1.1.

Related Work

The first step in generating a 3-D histology volume is to cut a series of very thin sections from tissue that has been embedded in a paraffin wax block. These sections are placed on glass slides, stained, and then scanned to generate digital WSIs. The placement of the tissue section onto the slide is not a precise process and the resulting image is affected by random in-plane translations and rotations, which have to be corrected for using rigid 2-D registration. In addition to this misalignment, folds, tears, and nonrigid deformations often occur during cutting, mounting, and staining the tissue sections and these must be corrected for using 2-D deformable registration. The final step in 3-D histology reconstruction involves stacking the 2-D images with the appropriate slice separation to form a volume and, in some cases, correcting for through-plane misalignment.

Several approaches for correcting the 2-D misalignment and deformations have been described. Some groups have used extrinsic fiducial markers to align the slices,^8,14 however, this is an invasive procedure, which has the potential to affect the pathologists’ ability to interpret the histological sections, and is frequently not permitted on clinical specimens.

Both intensity- and landmark-based registration methods have the advantage that they do not interfere with the appearance of the tissue sections. Intensity-based methods have been shown to be very effective in medical image registration but they may fail in histology, where the intensities across histology images are not constant.^15–17 Bağci et al.^18,19 have demonstrated that intensity variations across images can lead to registration errors and this problem cannot be fixed through a simple intensity normalization approach. Feature-based image registration techniques^20,21 rely on identifying corresponding features such as points and lines in both images, and the choice of a feature space plays a significant role in registration quality. Scale-invariant feature transform (SIFT) features²² take into account the spatial information obtained from the gradient of the pixel intensities and are invariant to brightness, rotation, and scale making them a suitable choice for use in histology.

Many 3-D reconstruction methods rely solely on the information from the series of 2-D histology sections and either register slices one to another,^15,23,24 or to a single reference section. ^16,18,25 These methods assume that structures visible on one slice are still present in the adjacent slices but this may not be true if the separation between them is too great. Also local distortions of the histology sections, such as shrinkage, expansion, tears, and folds, which occur during the histological preparation procedures, reduce the similarities between consecutive sections and consequently make the alignment of the 2-D images much more challenging. To overcome this problem, some groups have made use of in vivo image, acquired before the tissue is removed, to constrain the 3-D reconstruction of the histology slices.^10,11 This, however, is only possible if medical images are available and if it is possible to identify corresponding structures in both the histology and the in vivo images.

In our previous work,^3,26 we developed a pipeline for histology volume reconstruction, which used optical blockface images as reference images. Blockface images were obtained by photographing the surface of the tissue block before each section was cut, and the image of each histology section was then registered to its correspondent blockface image using 2-D rigid and deformable registration techniques. This is a practical solution when it is not feasible to densely sample the tissue using a small interslice separation and reference 3-D volumetric images of the specimen are not available. An edge-based registration method made use of points at the boundary between the tissue specimen and the surrounding paraffin block to carry out a rigid registration followed by a nonrigid deformation. We used implanted fiducial markers²⁷ to measure the registration accuracy in mouse xenograft specimens and found that the deformable registration generated using the boundary points actually degraded the accuracy of the global rigid registration.²⁶ This highlights the need to improve the deformable registration step in the pipeline.

As mentioned earlier, the goal of our work is to generate 3-D histology volume reconstructions from whole-mount breast lumpectomy images, where the highly deformable nature of breast tissue and the lack of clear boundaries and anatomical structure make this a particularly difficult problem. Clarke et al.¹³ demonstrated that manually identified landmarks can be used to align a whole-mount lumpectomy histology image with a specimen cone-beam computed tomography slice and used this manual alignment to compare 3-D with 2-D tumor measurements,¹² but this is a laborious and imprecise process. Booth et al.⁴ investigated the use of automated 3-D reconstruction of small breast tissue WSIs in the study of the biology of DCIS. They reconstructed the histology volume by selecting the middle section as the reference image and registering the neighboring sections to this reference image using the sum of squared differences of the neighboring pixel intensities.²⁸ This registration proceeded from the center out with subsequent sections aligned to their neighbors and it relied on having sequential $4\text{-}\mu \mathrm{m}$-thick sections making it impractical for use with whole-mount images. Reis et al.²⁹ investigated the maximum spacing between breast histology sections required for 3-D histology reconstruction to a specific tolerance, focusing on the accuracy of reconstruction of individual ductal structures that were extracted from the WSI. They also selected the section at the center of the block as the reference image and used a pairwise rigid or affine registration approach to align the sections to the reference image. They concluded that a spacing of $41\mu \mathrm{m}$ between sections was sufficient to assess ductal structures. However, in the clinical setting, the spacing between the breast sections is about 4 mm and methods that rely on slice-to-slice registration will likely fail.

1.2.

Our Approach

Our goal, therefore, is to develop an automated method for generating 3-D histology volumes that can be applied to whole-mount breast lumpectomy or mastectomy specimens without manual intervention and without relying on closely spaced serial sections. This paper focuses on the first step in a 3-D volume reconstruction pipeline, which is the correction of deformations in the whole-mount images using a reference blockface image. In our previous work, we automatically identified points at the boundary between the tissue specimen and the surrounding paraffin block in both histology and blockface images and used these to generate a deformation field,²⁶ but the results were disappointing. Here, we propose the use of an automatic feature-based image registration method, SIFTFlow, developed by Liu et al.,^30,31 to align the whole-mount and blockface images. Using SIFT features which are invariant to brightness, rotation, and scale eliminates the shortcoming of the intensity-based methods, and by establishing a very dense set of corresponding points we hope to improve on our previous method which only used sparsely sampled edge points. We investigate the accuracy of the SIFTFlow algorithm as a function of the parameter settings used and then optimize these parameters for our specific application using fiducial markers implanted in a lumpectomy specimen to assess registration errors. Finally, we compare the performance of the proposed deformable registration method with the edge-based method described previously.

Further processing steps to align the blockface images are required to complete the 3-D volume reconstruction once the deformations in the whole-mount images have been corrected. Large breast tissue specimens have to be cut into 4-mm-thick slices before paraffin embedding is carried out to facilitate tissue processing, which means that each whole-mount section is cut from a different block and additional tissue processing steps are required to realign the blockface images. We will report on the results of 3-D volume reconstruction in future work as a description of the full reconstruction pipeline is beyond the scope of this paper.

2.1.

Image Data

Two sets of image data were acquired which we will refer to as the training set and the test set. The training set of 10 whole-mount/blockface image pairs came from a single specimen and was used to determine an optimum set of parameters for the SIFTFlow algorithm and to carry out the comparison with the edge-based approach. The test dataset, comprising five image pairs from five different patients, was used to test the registration accuracy obtained using the optimized SIFTFlow method.

For the training data, we were able to obtain Institutional Research Ethics Board approval to implant multimodality fiducial markers into part of a lumpectomy specimen from a patient with invasive ductal carcinoma (the rest of the specimen was retained in the anatomic pathology laboratory for routine clinical assessment). Four multimodality fiducial markers were implanted in the fresh tissue using a biopsy needle.²⁷ The specimen was suspended in 3.5% agar gel and four additional fiducial markers were placed in the agar gel close to the specimen; these markers could not be used for the histology to blockface registration as the gel tended to become detached from the tissue during sectioning. The fresh tissue was sliced at 4 mm. Figure 1(a) shows one slice of the fresh tissue with the fiducial markers both in agar gel and the specimen. The tissue slices were then formalin fixed, processed, and embedded in paraffin⁶ to produce 10 blocks. One $4\text{-}\mu \mathrm{m}$-thick whole mount section was obtained from each paraffin block.

Fig. 1

(a) 4-mm slice of the fresh tissue, (b) blockface image (90-deg angle), (c) blockface image (oblique angle), and (d) H&E-stained whole-mount image.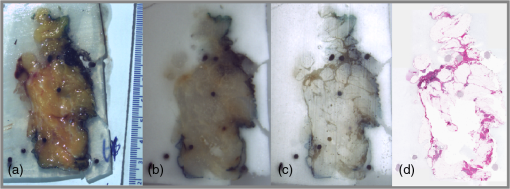

Immediately prior to cutting each section, a blockface image was captured using a telecentric lens. Imaging the blocks at a 90-deg angle provides an image with low contrast between the tissue at the surface of the block and the surrounding paraffin and also between different tissue types [Fig. 1(b)]. Positioning both the lens and light source at an oblique angle ($\approx 15\text{-}\mathrm{deg}$ from 90-deg angle) produces a high-contrast image [Fig. 1(c)], but introduces a horizontal scaling artifact. We correct this by calculating a scaling factor based on the horizontal distances between the fiducial markers in the gel. After applying the scaling correction, the oblique blockface images are used as reference images. The pixel size of the blockface images was $186\mu \mathrm{m}$ and the corrected blockface images were cropped to $340\times 410\text{pixels}$ to remove excessive background.

The tissue sections were stained with hematoxylin and eosin (H&E), which provides good contrast between fibroglandular tissue (purple), stroma (pink), and fatty tissue (mostly white), and is the most commonly used histological stain. They were then digitized at $2\text{-}\mu \mathrm{m}$ resolution, downsampled to the resolution of the blockface images, and padded with the average background pixel values to the size of blockface images [Fig. 1(d)].

For validation, a testing set of five pairs of blockface and histology images were also acquired from lumpectomy specimens from five different patients with the Institutional Research Ethics Board approval. It was not possible to get approval to implant fiducial markers in these specimens and only a single section was used from each specimen. A smaller lens was used to obtain the blockface images for these testing images, therefore, the resolution of blockface images and the downsampled whole-mount images was $55\mu \mathrm{m}$.

2.2.

Registration Using Scale-Invariant Feature Transform Features

Dense SIFT features^22,31 are used, in this work, to find the rotation and translation of the histology images with respect to their correspondent blockface images. For each pixel, an eight-bin histogram of gradient orientations is calculated for 16 $4\times 4\text{pixels}$ neighboring blocks, which results in $8\times 16=128$ features. Therefore, for each $w\times h$ image, we have a 3-D SIFT image of dimension ($w\times h\times 128$).³⁰

2.2.3.

SIFTFlow parameter optimization

Liu et al.^30,31 do not discuss their choice of regularization parameter values in their papers, suggesting that the default parameter settings of $\eta =0.005$, $\alpha =2$, and $d=40$ used in their software implementation³³ were suitable for the many image types used in Ref. 31 to illustrate the SIFTFlow method. Our task of registering breast histology images to blockface images, however, is very different from that of registering natural images due to the presence of tears, folds, and other artifacts in the histology slices and it is necessary to determine what effect the parameter settings have on registration accuracy and also to identify the most appropriate settings to use.

We developed the iterative optimization method summarized in Fig. 2 to determine the most appropriate parameter settings for lumpectomy specimens. In the first step, the objective function [Eq. (2)] is minimized to find the displacement field using the initial parameter values from Ref. 33. In this step, the efficient belief propagation method^31,34 is used to find the deformation field. In the second step, the objective function is optimized using the Nelder–Mead optimization algorithm to find updated parameter estimates for the displacement field obtained from the first step. The new estimated parameters are then used as inputs for the first step to find a new displacement field. These two steps iterate until either the change of the function value is lower than an upper limit or it reaches a maximum number of iterations.

Fig. 2

Flow chart outlining the joint parameter optimization method.

We carried out this parameter optimization on the training data set. Leave-one-out cross-validation (LOOCV) was adopted, i.e., the parameters were estimated using nine pairs of images and then tested on the image which was left out. The formulated objective function with LOOCV is shown as follows:

Eq. (3)

$$\begin{gathered} \text{Minimize}:E(\omega )=\sum _{n\text{Image}}(\sum _p{\Vert S_1(p)-S_2[p-\omega (p)]\Vert }_1 \\ +\sum _p\eta [|u(p)|+|\upsilon (p)|] \\ +\sum _{(p,q)\in ϵ}\{\min [\alpha |u(p)-u(q)|,d]+\min [\alpha |\upsilon (p)-\upsilon (q)|,d]\}). \end{gathered}$$

The summation on $n\text{Image}$ is added for LOOCV.

To make sure that the optimization was not influenced by the presence of the fiducial markers, the regions of the images with fiducial markers were marked manually for each pair of histology and blockface images after the rigid alignment of the images and then excluded from the calculation of the objective function.

2.3.

Registration Using Edge Points

In previous work, we used an edge-based registration method^3,26 to align histology and blockface images from smaller murine tissue blocks. Here, we apply the same method to the whole-mount lumpectomy images to make a comparison with the SIFTFlow method. For the initial affine registration step, the segmented boundary points are aligned using Fourier descriptors^35,36 and then the registration is refined using the iterative closest points³⁷ algorithm. The aligned boundary points are then used as control points to find the nonrigid deformation, and a thin-plate spline is used to model the deformation field.

The edge-based approach is simple to apply when there is a good contrast between the tissue and background in both histology and blockface images. In breast histology images, however, there is very low contrast between the fatty tissue and the background, which makes the automatic segmentation of the boundary points very challenging. Therefore, in this work, we manually segmented the boundaries of the tissue in both sets of images.

2.4.

Validation

The rigid alignment of the image pairs in the training set was assessed by measuring the mean target registration error (TRE) based on the center of the four fiducial markers implanted in the specimen. To measure the deformable error, we also selected some internal landmarks in each pair of images and calculated the mean TRE based on these internal points. We attempted to identify an equal number of evenly distributed landmarks in each image pair for both the training and the testing datasets.

3.1.

Affine Registration

Rigid and affine registrations were carried out using the SIFT feature-based method described in Sec. 2.2.1 and the edge-based method described in Sec. 2.3. Figure 3 shows an example of one pair of blockface and histology images together with the aligned histology images obtained by using the edge- and the feature-based methods, respectively. The large amount of fatty tissue leads to very poorly defined tissue boundaries, particularly in the histology images, and it was necessary to manually define boundaries for the edge-based approach.

Fig. 3

Rigid registration of a histology image to the corresponding blockface image: (a) blockface image with boundary in blue (figure best viewed in color) and (b) histology image with manually defined boundary shown in red and blockface boundary in blue. Aligned histology images: (c) using edge-based method and (d) using dense SIFT features. The boundary of the blockface image is overlaid on both aligned histology images for comparison.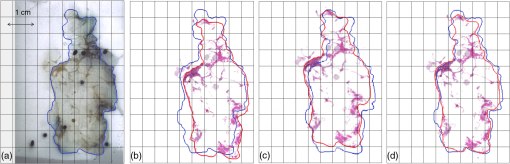

The TRE calculated using the center of the implanted fiducial markers in the tissue is reported in Table 1. The improvement in TRE when using dense SIFT feature-based method is small with respect to the edge-based method, but the feature-based method has the advantage that it is not dependent on image segmentation. The results in Table 1 also show that using a similarity transformation, which allows for scaling, improves the alignment compared with a simple rigid transformation.

Table 1

TREs for rigid and affine registration. Values are the mean TREs (± stdev) based on implanted fiducial markers.

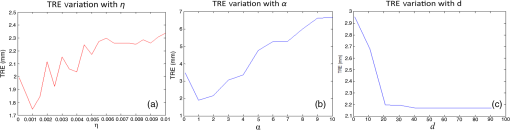
3.2.

Deformable Registration

3.2.1.

Effect of regularization parameters on SIFTFlow registration

Figure 4 illustrates the effect of changing the parameters controlling the magnitude of the displacement of the pixels $\eta$ and the smoothness of this displacement $\alpha$. White areas on the images represent regions where compression has occurred.

Fig. 4

The deformation fields calculated with different settings for $\eta$ and $\alpha$ are applied to a grid image to visualize the effects of changing the regularization parameters. Increasing $\alpha$ results in smoother displacement: (a) $\eta =0.005$, $\alpha =1$ and (b) $\eta =0.005$, $\alpha =2$. Increasing $\eta$ results in smaller displacements: (c) $\eta =0.0005$, $\alpha =2$ and (d) $\eta =0.1$, $\alpha =2$. Parameter $d$ was fixed at the default value of 40 in all cases.

The effect of changing each of the regularization parameters was assessed by holding two of the parameters fixed at the default values and then varying the third parameter. The plots in Fig. 5 show the mean TRE calculated using the fiducial markers in all 10 training image pairs as each parameter is varied over a range of values. We see that the largest variation is caused by changes in $\alpha$, the smoothness parameter, and Fig. 5(c) suggests that changing $d$ has very little effect once $d>20$. We, therefore, kept $d$ fixed at the default value of 40 when carrying out the multivariate optimization outlined in Sec. 2.2.3.

Fig. 5

Sensitivity of TRE (measured using the implanted fiducial markers) to the SIFTFlow parameters: (a) $\eta$, (b) $\alpha$, and (c) $d$.

3.2.2.

Identifying paired landmarks for the assessment of deformable registration

Most of the landmarks were selected at the corners of the fibroglandular tissue and a few at the cross section of the blood vessels, where the correspondence of the points in histology and blockface images could be determined. It was not possible to identify landmarks in the fatty tissue with confidence. Figure 6 shows two pairs of blockface and histology images. The smaller section contains mostly fat, while the larger section has more fibroglandular tissue making it possible for more landmarks to be identified. The number of manually selected landmarks varied for different sections in the training dataset as there was a wide variation in section size and composition and, although we attempted to evenly distribute landmarks throughout the images, this was not always possible as can be seen in Fig. 6. The number of landmarks in the 10 training sections varied from 4 to 10.

Fig. 6

Two pairs of blockface and histology images with different sizes and composition. Top row shows the (a) blockface and (b) histology images of a small section, which mostly contains fat. Bottom row shows the (c) blockface and (d) histology images of a larger section with more fibroglandular tissue and higher number of selected landmarks. The arrows on the blockface images show the selected landmarks.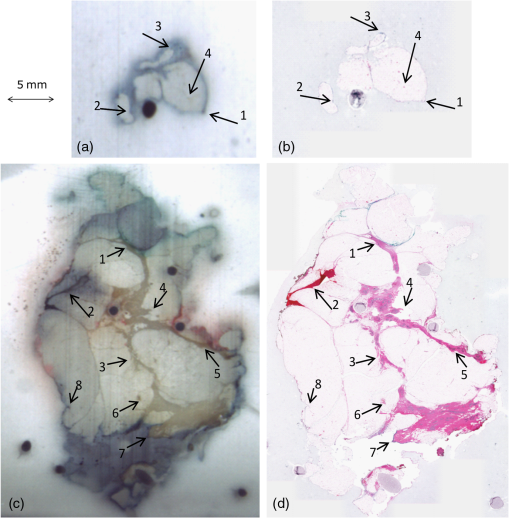

The five sections taken from five different patients were all selected through the center of the specimens and as well as being larger, they also contained more fibroglandular tissue allowing us to identify 10 landmarks in each test image pair.

3.2.3.

Comparing edge-based deformable registration with SIFTFlow

The procedure outlined in Fig. 2 was used to estimate the optimum parameters $\eta$ and $\alpha$ in the SIFTFlow objective function ($d$ was fixed at 40 throughout). The optimized parameters and the associated mean TREs (calculated using both the implanted fiducials and the manually defined landmarks) from the LOOCV experiment using 10 pairs of images are reported in Table 2.

Table 2

Average TREs for LOOCV experiment using edge-based SIFTFlow with default parameters, and SIFTFlow with optimized parameters measured using both fiducial markers and manually selected landmarks. Values are given as mean (stdev) in mm.

				Mean TRE (mm) Fiducial markers			Mean TRE (mm) Manual landmarks
Case no.	η (10−3)	α	No. of landmarks	Edge based	Default SIFTFlow	Optimized SIFTFlow	Edge based	Default SIFTFlow	Optimized SIFTFlow
02	5.185	1.149	5	7.46 (0.00)	8.09 (0.00)	7.56 (0.00)	6.82 (0.00)	7.83 (1.80)	6.24 (1.50)
03	5.397	1.129	5	3.1 (0.00)	3.03 (0.00)	0.41 (0.00)	2.97 (0.00)	3.86 (0.95)	0.43 (0.07)
04	5.283	1.137	8	5.39 (0.57)	1.56 (1.78)	0.27 (0.05)	5.13 (1.10)	1.50 (1.53)	0.71 (0.93)
05	5.279	1.137	10	1.22 (0.63)	0.44 (0.49)	0.36 (0.54)	1.09 (0.74)	0.80 (0.88)	0.79 (0.90)
06	5.080	0.913	10	0.54 (0.28)	0.46 (0.25)	0.17 (0.16)	0.98 (0.31)	1.17 (1.60)	0.79 (1.12)
07	5.125	1.160	10	1.38 (0.67)	0.43 (0.22)	0.22 (0.16)	1.14 (0.53)	0.44 (0.63)	0.30 (0.19)
08	5.215	1.149	8	1.56 (0.32)	1.07 (1.17)	0.24 (0.06)	1.52 (0.40)	0.79 (0.70)	0.37 (0.15)
09	5.442	0.862	5	1.89 (0.15)	0.81 (0.64)	0.25 (0.23)	1.78 (0.20)	1.10 (1.25)	0.56 (0.18)
10	5.125	1.160	4	0.81 (0.00)	0.19 (0.00)	0.19 (0.00)	0.76 (0.00)	0.21 (0.15)	0.22 (0.15)
11	5.282	1.137	4	077. (0.00)	0.45 (0.00)	0.18 (0.00)	0.68 (0.00)	0.52 (0.53)	0.51 (0.51)

In case no. 02, the error is very high; this is because a part of the tissue section is missing on the histology slide leading to a large discordance between the stained section and the corresponding blockface image.

For the TREs measured using fiducial markers, the results confirm that optimizing the regularization parameters significantly improves registration accuracy ($p=0.0088$ using a paired two tailed $t$-test, normal distribution of TREs was confirmed using a Kolmogorov–Smirnov test). The average difference between the TRE obtained from the optimized and default parameters is 0.67 mm, which corresponds to $\sim 4\text{pixels}$ at $186\text{-}\mu \mathrm{m}$ resolution.

The results of the deformable registration using the edge-based method are also shown in Table 2. Errors were significantly higher than those obtained with the SIFTFlow method.

Figure 7 shows one of the blockface images and the corresponding histology image after registration with each of the methods tested. The circle in Figs. 7(a) and 7(b) highlights an area of tissue that is missing on the histology slides. In Fig. 7(b), a part of the tissue is missing and the segmented tissue boundaries are different in the histology and blockface images, resulting in poorer performance of the edge-based registration method compared to the feature-based method. It has also been noticed that with the edge-based method, as expected, the structures closer to the edge of the tissue are generally better aligned than the structures further away from the boundary points. In Figs. 7(c) and 7(d), arrows point out areas of difference in the default and optimized SIFTFlow results.

Fig. 7

Images from case no. 04: (a) blockface image and (b) histology registered using edge-based method; the circle shows a missing part of the tissue section in histology image, which can degrade the result of the registration. c) Histology registered using default SIFTFlow parameters and (d) histology registered using optimized SIFTFlow. The arrows point to some of the areas that are more accurately registered when the optimized parameters are used.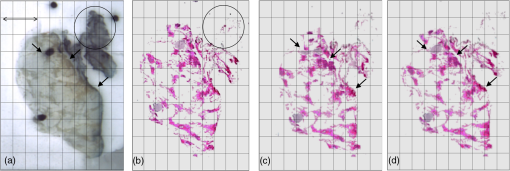

To obtain a single set of SIFTFlow parameters to use in the test dataset, we repeated the optimization procedure using all 10 image pairs and obtained values of $\eta =4.9\times {10}^{-3}$ and $\alpha =1.169$.