|
|
1.IntroductionOptical tomography1–8 is known as a safer alternative to x-ray tomography. Usually, tomography consists of a light source generating penetrative light and a detector capturing the light, which allows to estimate the inside of the object through which the light is passing. The most important application is x-ray computed tomography (CT), where x rays are used due to their penetrative property. The balance between the radiation exposure of the human body and the quality of the obtained results has been debated since the early days when x-ray CT was invented. Therefore, there is an urgent demand for a safer medical tomography, such as optical tomography. Modeling the behavior of light plays an important role in optical tomography, and in the mesoscale, in which the wavelength of light is close to the scale of tissue, the radiative transport equation (RTE) is used for describing the behavior of light scattering.5,9 At the macroscale,6 the time-independent or dependent RTE is often approximated with a diffusion equation. Similarly, the computer graphics community has the used time-independent RTE, and in contrast to the (surface) rendering equation,10,11 often calls it the volume rendering equation (VRE).10,12 and the notations will be introduced in the following sections. The use of VRE enables us to render volumes of participating media, such as fog, cloud, and fire through which light is penetrating, and to obtain realistic volume rendering images of such scenes.13,14 The path integral, which can be considered as a discrete version of the continuous Feynman path integral,15,16 has been recently employed to solve the VRE in an efficient way with Monte Carlo integration, such as Metropolis light transport17,18 or bidirectional path tracing.19In this paper, we propose an optical tomography method using path integral as a forward model and solving a nonlinear inverse problem that minimizes the discrepancy between measurements and model predictions in a least-squares sense. To the best of our knowledge, the discretized path integral has not been used in optical tomography before. In our work, we simplify the path integral with some assumptions. The path integral, as the name suggests, gathers (or integrates) the contributions of all possible paths of light.17,18,20–23 We approximate the integral of an infinite number of paths with the sum of a finite number of paths, discretize a continuous medium into voxels of a regular grid, and continuous light paths into discrete ones (i.e., polylines). We deal with anisotropic scattering having a peak in the forward direction, which is different from other discretization methods using discrete ordinate or spherical harmonics.13,24,25 In this work, we focus on estimating the spatially varying extinction coefficient at each discretized voxel location of the medium while fixing scattering properties (e.g., scattering coefficients and phase functions ). By separating the scattering properties from our problem, we formulate optical tomography as an optimization problem with inequality constraints solved by an interior point method. An interior point method26 is an iterative method to solve an optimization problem with inequality constraints describing a feasible region in which the optimal solution must reside. To this end, a series of nonconstrained optimization problems are constructed by combining the constraints and the original objective function and are solved by an ordinal gradient-based (Quasi-Newton) method. To summarize our contribution, we reformulate the problem of optical tomography by combining a path integral with several simplifying assumptions to model the light transport in the participating media. This paper is an extension of our previous conference version27,28 with additional theoretical background and additional experiments and discussions, and is structured as follows. In Sec. 2, we briefly review previous work related to path integrals and optical tomography. In Sec. 3, we describe how to model the light transport in participating media and turn optical tomography into an optimization problem. In Sec. 4, we show how to solve the optimization problems. Section 5 reports some simulation results, and Sec. 6 concludes the paper. 2.Related WorkIn this section, we briefly review related work on optical tomography and path integrals in computer graphics. Optical tomography4,5 (or inverse transport,6,7 inverse scattering,29 scattering tomography30,31) is a problem in medical imaging using light sources to reconstruct the optical properties of tissue from measurements (time-dependent or stationary, angular-dependent or independent) at the surface boundary. Analytically solving the RTE [Eq. (1)] with boundary conditions is difficult, however, and approximations, such as discrete ordinates and ’th-order spherical harmonics ( approximation), are often used and solved numerically by, for example, finite element methods (FEM) or finite difference methods. The famous diffuse approximation5,6 (DA) is a (thus first-order) approximation with the assumption on a phase function being isotropic. The DA is an approximation to RTE at a macroscopic scale when scattering is large while absorption is low and scattering is not highly peaked. Diffuse optical tomography (DOT) is based on DA and today represents the frontier of optical tomography32,33 with many clinical applications.34 DA, however, does not often hold in realistic participating (scattering) media; absorption may not be small compared to scattering, and the shapes of the phase functions can be highly peaked in the forward direction, which is often modeled by Henyey-Greenstein,35 Schlick,36 or Mei and Rayleigh phase functions.10,12,37,38 Experimental evidence39 also suggests a highly peaked shape of the phase functions in biological media. DOT works, but is still limited; therefore, other methods have also been studied for cases when DA does not hold. Statistical Monte Carlo methods are used for media in which the assumptions do not hold; however, they are computationally intensive and inefficient for solving the forward problem,4–7,34 i.e., solving the RTE with given parameters. Therefore, Monte Carlo based approaches have been used for estimating the spatially constant (not varying) parameters in homogeneous media, such as paper,40,41 clouds,42 liquids,43 plastics,44 or uniform material samples.45 Another difficulty of Monte Carlo based inverse methods is that an analytical forward model prediction is hard to obtain when we want to minimize the difference between the prediction and measurements except for very special structures.46,47 A gradient based least-square approach has been proposed but only for spatially constant parameter estimation,40,41,48 while model-free approaches have relied on genetic algorithms,42,44 numerical perturbation,49,50 voting,51 or even simple backprojection.52 One of the contributions of the current paper is to enable us to use a gradient based optimization approach for estimating spatially varying parameters, which is extensible by using many optimization methods. Similar to optical tomography, modeling light transport plays a very important role in computer graphics. Our own work on optical tomography is inspired by Monte Carlo based statistical methods. In the last two decades, methods based on path integrals17–19,53–55 have provided models of light transport for efficient volume rendering. For solving RTE, a path integral has been used for a forward problem solver,16,56,57 and has also been applied to optical tomography, but under the diffusion assumption.58,59 Our proposed method is based on a path integral to explicitly express the forward model prediction, which is very suitable for solving the inverse problem with gradient based methods. This is an advantage of our method over existing methods because the paths used in the forward model can be generated by either a deterministic or statistical (Monte Carlo) method. To achieve an efficient forward model, we introduce a simplified layered scattering model that uses a limited number of deterministic paths instead of Monte Carlo simulated ones. 3.Method: Forward ProblemWe deal with the following optical tomography problem [this is a conceptual formulation and the actual problem is shown in Eq. (29)]. where is a vector representing the spatial distribution of the extinction coefficients to be estimated. We divide our discussion into two parts: forward and inverse problems. The forward problem focuses on building a mathematical model of the light transport between a light source and a detector . We will make some assumptions on the light transport and the medium to simplify the forward model. An inverse problem minimizes the difference between the observations of the detector and the forward model to estimate the spatial distribution of the extinction coefficients .3.1.Forward ModelIn the forward problem, as we mentioned before, we use a path integral to build a mathematical model for the light transport. Here, we follow the notation developed in the computer graphics literature17,23,53,60 to introduce the path integral. Sections 3.2 to 3.6 will show the simplified model we propose. Given a space , a light source is located at and a detector at , and in between them is the participating media with boundary and interior volume . A light path connecting and of length consists of vertices for , denoted by . Thus, absorption, scattering, or reflection events happen at . The set of all paths of length is denoted by . The path space is the countable set of all paths of finite length. A direction is denoted by , where is a unit sphere in . A unit vector is the direction from vertex to vertex in a path . Veach20 introduced a framework representing the rendering equation in the form of a path integral for scenes without participating media (i.e., no scattering), and later, Pauly et al.17 extended it to the volume rendering equation with scattering. The amount of light observed by the detector is given by the path integral which is an integral over the path space. Here, is a measure of path . where denotes the differential measure at vertex . is a measurement contribution function defined as follows: where is the camera response function, and is the intensity of the light emitted from the light source to vertex . is a scattering kernel at with respect to the locations of vertices and .Here, the bidirectional scattering distribution function is used for locations on the surface of objects, and the scattering coefficient at and the phase function are used for those inside the medium. is a generalized geometric term. where is a geometric term. with unit normal of the surface at . is a transmittance that describes the attenuation when light passes through the medium. where is the extinction coefficient at vertex .Putting all together, we have a path integral of the following infinite sum of all possible path contributions. Note that all vertices depend on a path ; different paths have different sets of vertices. In the equation above, however, we omit the path index for simplicity. Later, we will again use as the path index. 3.2.Assumptions on the Path Integral FormulationAs our target is optical tomography, we restrict the model to deal with inside the participating media. To do so, we assume that the light source and detector are located on the surface, and the other vertices are inside the medium, that is, and . Then the transmittance is simplified as Furthermore, we assume that the observations are ideal and the camera response function is the identity, . Apart from the assumptions above, we rewrite the geometric term and the differential measure. The definitions above use area measures and volume measures along with the squared distance geometric term;17,23,53 however, steradian measures and the identity geometric term is equivalent and also widely used.10,12,60 Therefore, we employ the steradian measures and rewrite it as follows: Now, Eq. (12) is written as 3.3.Discretization of the Forward ModelFor numerical computation, we first discretize the medium into voxels of a regular grid, where each voxel has its own extinction coefficient ( is the index of the voxel) as shown in Fig. 1. Fig. 1Illustration of a discretization example. (a) Voxelization of the medium into a regular grid of size . Voxels are indexed in raster scan order in this example, from left to right, and top to bottom. Each voxel has extinction coefficient . (b) A path segment between vertices and . Voxels involved in the segment are shaded. (c) Lengths of the involved voxels . Here we denote instead of for simplicity. 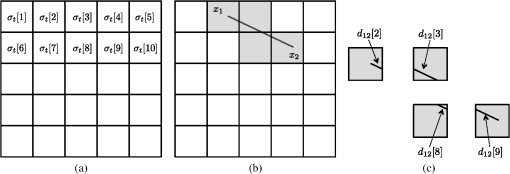 With this voxelization, the paths of light are also divided into segments, as explained below. First, we explain the integral [Eq. (11)] along a single segment of a path . It describes the attenuation of light along the segment due to the extinction coefficients of the voxels involved. Because of the discretization of the medium, Eq. (11) can be written as a sum of voxel-wise multiplications. For the second equality, is the index of a set of all voxels involved by segment , and is the length of the part of the segment passing through voxel . This is illustrated in Fig. 1(c). The extinction coefficient is now a piece-wise constant function because of the voxelization; then the integral turns into a sum (the idea that this integral can be turned into a sum has been discussed before,61 however, not in the context of tomography). This simplifies the computation; however, the sum over a set is not preferable in terms of implementation and optimization. We propose here to use a vector representation of both extinction coefficients and segment lengths, which is the third equality of the above equation. The first vector stores the values of the extinction coefficients of all voxels. This vector can be generated by serializing the voxels on the grid in a certain order. The second vector contains the values of the lengths for all voxels. We should note that this vector is very sparse; most of the voxels have no intersection with the segment . Hence, only a few elements in have nonzero values, and the other elements are zero because those voxels have no intersection and . This sparsity of the vector facilitates the construction of a whole path because path segments can be added as follows: where is the vector of a complete path of length ; the ’th element can be interpreted as the length of the segment when the path passes through voxel . This notation simplifies a part of Eq. (17) as follows:Using this notation to rewrite Eq. (17), we have where the factor , defined as describes the contributions of the scattering coefficients and phase functions, and the exponential factor represents attenuation due to absorption (and outscattering) over the path.3.4.Two-Dimensional Layered Model of Forward ScatteringAs a first attempt, we design a two-dimensional (2-D) layered grid, instead of the three-dimensional (3-D) one. Since we voxelize the medium into a regular grid, the 2-D medium consists of parallel layers. Hereafter, a 3-D direction between vertices is written as a 2-D direction and a steradian measure as an angular measure . As shown in Fig. 2, we assume a particular layer scattering having the following properties. First, vertices of path are located at the centers of each voxel. The light source is located on the boundary of the top surface of the voxels in the top layer. Similarly, the detector is located on the boundary of the bottom surface of the voxels in the bottom layer. Second, directions and at the beginning and end of a path are perpendicular to the boundary. This means that scattering begins at and ends at . Third, forward scattering happens layer by layer. More specifically, light is scattered at the center of a voxel in a layer and then goes to the center of a voxel in the next (below) layer. Scattering is assumed to happen every time the light traverses voxel centers. Even if the next voxel is just below the current voxel and the path segment is straight, it is regarded as scattering. Fourth, the scattering coefficient is uniform, . Fig. 2Proposed two-dimensional layered model of scattering. This example shows path consisting of vertices located at the centers of voxels in a grid with parallel layers. is a light source located on the top surface, and is a detector at the bottom. At each vertex, the light scatters to voxels in the next layer, and possible scattering directions are indicated by arrows. 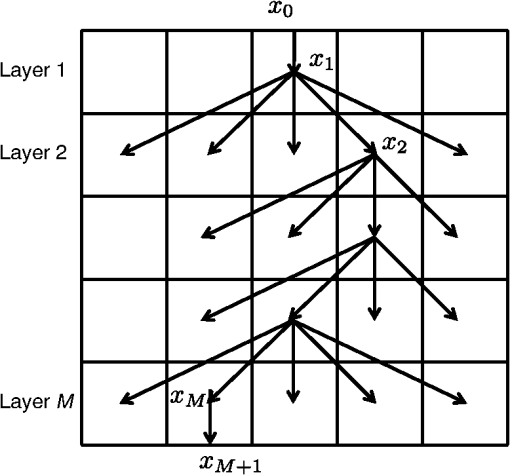 By ignoring paths exiting from the sides of the grid, the number of all possible paths is , where is the number of layers and is the number of voxels in one layer. 3.5.Approximating the Phase Function with a GaussianWe use a Gaussian model as an approximation of the phase function where the variance controls the scattering property; larger values of mean strong forward scattering. This Gaussian approximation is convenient in our case because of the following two reasons.First, existing phase function models10,12,35–38 are those for 3-D scattering, not for 2-D. This means that those functions are normalized for integrals over the unit sphere : . Most of the phase functions assume isotropy (rotational symmetry), and hence, the function has a form taking angle as an argument; however, . These functions, therefore, are not adequate for our case. Second, our assumption of layer-wise forward scattering does not allow scattering to happen backwards or sideways, and the Gaussian model is suitable for it. As shown in Fig. 3, the Gaussian model has the form of forward-only scattering (no backwards or sideways) in a reasonable range of , and it is almost normalized; . Other 2-D phase functions exist which are not forward-only. For example, Heino et al.62 introduced a 2-D analog of Henyey-Greenstein’s phase function,35 shown in Fig. 3. Although the parameters are different, the two functions in Fig. 3 have similar shapes. The most important difference is that Heino’s function has backward scattering, but our Gaussian model does not. More realistic scattering rather than the layer-wise forward scattering introduced here needs Heino’s or Henyey-Greenstein’s phase function. Fig. 3Comparison of two-dimensional phase functions. The upward vertical direction is , and horizontal directions are . (a) Gaussian approximated phase functions with . The tallest and narrowest shapes correspond to , and the shape becomes shorter and rounder for larger values of . (b) Heino’s two-dimensional analogs62 of Henyey-Greenstein’s phase function with parameter . The tallest and narrowest shapes correspond to , and the shape becomes shorter and close to a hemisphere for smaller values of . 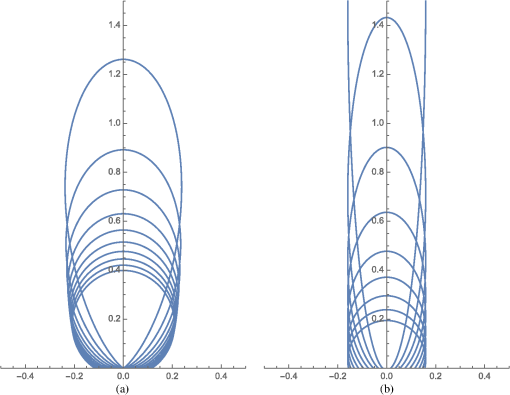 We should note one further simplification in our layer-wise forward scattering model. The angle in the phase function is usually defined between and , that is, the difference of directions changed by the scattering event. Instead of dealing with such an exact difference of directions, we use the angle between and the vertical (downward) direction for efficiency of computation. This assumption enables us to discretize the Gaussian phase function much more easily. Since integrates to (approximately) one, such a normalization can be discretized with a sum as follows: where is a set of voxel indices in the next layer , is an alternative form of the corresponding , and is the angle measure as shown in Fig. 4.Fig. 4An illustration of angle measure for voxel in the next layer. For the center voxel of the upper layer, voxel (shaded) in the next layer subtends an angle of , which is used for the angle measure in Eq. (24). 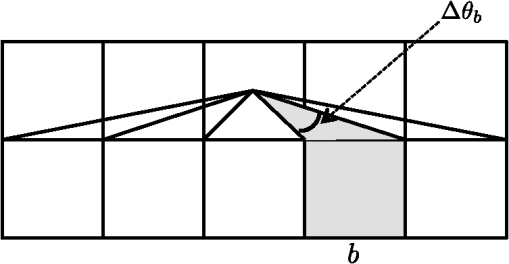 The above equation can be considered as the energy distribution from a voxel in one layer to the voxels in the next layer. For a voxel at direction , the value of describes what percentage of the energy will be scattered to this voxel. Figure 5 shows plots of the values corresponding to two phase functions with different parameters. We can see that, due to forward scattering, most of the energy is concentrated in the voxel just below, and a small part goes to the adjacent voxels. Fig. 5(a) The phase functions with parameter (dashed line) and (solid line). Plot of the value for each voxel for (b) and (c) . Note that index is relative to the voxel in the next layer just below the voxel in consideration. The voxel just below is , the voxel on its right side is , and that on the left side is . 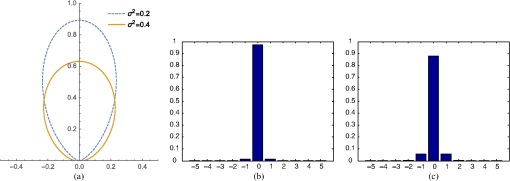 The contribution in Eq. (22) now needs to be rewritten so that it deals with the Gaussian phase function and the discretized energy distribution discussed above. First, we reorder the measure and then replace the factors with the Gaussian phase function.Note that the factor is common for all paths because we assumed that the grid is uniform so that is constant, and the direction (or ) is perpendicular to the top surface, and is constant. 3.6.Observation ModelSuppose the 2-D layered medium is an grid; it has layers, each of which is made of voxels. We now construct an observation model of the light transport between a light source and a detector: emitting light to each of the voxels at the top layer, and capturing light from each voxel from the bottom layer. More specifically, let and be voxel indices of the light source and detector locations, respectively. By restricting the light paths to only those connecting and , the observed light is written as follows: where and are the same as in Eqs. (27) and (21), respectively, but are restricted to paths connecting and , and assuming the light source to be constant.In the above equation, indexes the light paths, which share the same and . Due to the layered scattering model in the grid, the number of different paths between and is . This is, however, too large even for small and , e.g., . Therefore, we exclude paths having small contributions from the computation. This is done by a simple thresholding while computing as shown in Algorithm 1. This results in generating fewer paths; . For example, there are paths for with when , which enables us to reduce the computation cost. Algorithm 1Computing contribution Hijk and omitting low contribution path by thresholding.
4.Method: Inverse ProblemNext, we propose a method for the inverse problem of the forward model [Eq. (28)] to estimate the extinction coefficients of the 2-D layered model. As we mentioned before, we fix the light paths and assume that the scattering coefficients and parameters of the Gaussian phase function are uniform and known in advance. 4.1.Cost FunctionIn the 2-D layered medium described in Sec. 3.6, we had assumed a configuration of a light source and detector similar to the left-most one shown in Fig. 6; the light source is located above the medium and the detector is below, and the observed light is , where are the voxel indices of the light source and detector locations. By sliding the light source and the detector, we can obtain observations, resulting in the following least-squares equation: under constraints where denotes the generalized inequality, i.e., all elements in the vector must satisfy the inequality. The lower bound 0 comes from the fact that any media must have positive extinction coefficients, while the upper bound is used for numerical stability to exclude unrealistic values to be estimated.Fig. 6Four configurations of light sources and detectors. From left to right, we call configurations T2B (top-to-bottom), L2R (left-to-right), B2T (bottom-to-top), and R2L (right-to-left), which represent locations of light sources and detectors. 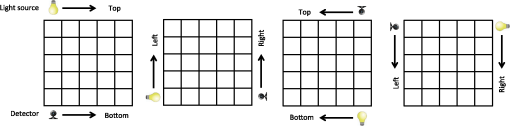 Furthermore, as shown in Fig. 6, we have four configurations of light sources and detectors by changing their positions. This gives us four different sets of observations and paths . These four different sets lead to four objective functions (, , , ) as shown in Fig. 6. Since the four objective functions share the same variables , we can use all of them at the same time by adding them to form a new single function at the expense of additional (factor of four) computation cost. 4.2.Optimization Problem with Inequality ConstraintsSince the inverse problem [Eq. (31)] is nonlinear, we employ an interior point method,26 an iterative optimization algorithm for problems with constraints. Here, we first review several key points in optimization; then we will develop an algorithm to solve Eq. (31) along with the required first- and second-order derivatives of the cost function. 4.2.1.Unconstrained problem: Quasi-NewtonFirst, we review optimization without constraints, which is used inside the interior point method. The general form of unconstrained optimization is where is a real vector and is an objective function that is twice continuously differentiable.To solve it, an iterative procedure begins with an initial guess and generates a sequence . It stops when the change of solutions is small enough. The information about function at or even previous estimates is used to calculate a direction to move with a step size . A line search is often used to determine the step size by searching along the direction starting from for finding with the least value of the objective function Once we find the step size, the estimate is updated as . The direction is for the Newton’s method, where is the inverse of the Hessian. The Newton’s method is well known for its second-order convergence and accuracy. However, when the dimension of the problem is large, calculating the Hessian and its inverse is computationally expensive. Therefore, Quasi-Newton methods are often used, where the inverse Hessian is updated by incremental approximations in order to reduce the computation cost. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) update rules are well known.63 When the conditions and (where means positive definite) are satisfied, the BFGS update guarantees the positive definiteness of . Algorithm 2 shows the Quasi-Newton method. Algorithm 2The Quasi-Newton method with BFGS update rule.
4.2.2.Constrained problem: interior pointHere we introduce a constrained optimization with inequality constraints of the form where is a real vector and are twice continuously differentiable.The idea is to approximate it as an unconstrained problem. Using Lagrange multipliers, we can first rewrite Eq. (37) as where is an indicator function, which keeps the solution inside the feasible region.Equation (38) now has no inequality constraints, while it is not differentiable due to . The barrier method26 is an interior point method that introduces a logarithmic barrier function to approximate the indicator function as follows: where is a parameter to adjust the accuracy of approximation. The log barrier function goes to infinity rapidly as goes close to 0, while it is close to 0 when is far away from 0. Since is differentiable, we have or equivalently,The barrier method solves Eq. (42) iteratively by increasing the parameter . At the limit of , the above problem coincides with the original problem [Eq. (38)]. 4.3.Algorithm for Solving the Inverse ProblemAlgorithm 3 shows our algorithm, which uses a barrier method with Quasi-Newton for solving the inverse problem. We should mention the following parts where we have modified the original algorithm.26 Algorithm 3Barrier method of interior point with Quasi-Newton solver.
Warm start: For each inner loop, the Quasi-Newton method needs an initial guess of the inverse Hessian . Instead of fixing for every inner loop, we reuse the of the last inner loop to accelerate the convergence (shown in lines 4 and 19 in Algorithm 3). Checking feasibility: Since the Quasi-Newton method and line search estimate without constraints, the next estimate may go beyond the constraints; in our case, each element in must be inside after the step size has been determined. Therefore, in line 8, we check the feasibility of the estimate for the current step size . If it exceeds the boundary of the feasible region, we pull the estimate back into the feasible region by halving the step size. If it is still outside the feasible region, then the step size is halved again. Why do we not just set the step size so that is exactly on the boundary? The reason is the log-barrier: if is on the boundary, in other words, is either 0 or , then or becomes infinite, which results in numerical instability. Therefore, the procedure described above is needed. Checking for positive definiteness: The BFGS update rules guarantee to be positive definite if and are satisfied. While the latter is satisfied by giving an appropriate initial guess, the former depends on the updates at each iteration. If it is not satisfied, then the BFGS updates are no longer valid, and we reset the inverse Hessian to a scaled identity63 at line 16. 4.3.1.JacobianHere, we represent the Jacobian of the objective function in Eq. (29). Note that the objective function in Eq. (31) can be derived in the same manner. We first rewrite the objective function as follows: and the gradient of is given byTo simplify the equation, we use the following notation: Now, and the gradient can be represented as where stands for the sum over the elements of the container [Eq. (49)] of vectors, is the element-wise product, and denotes the tensor product, defined as5.Numerical SimulationsIn this section, we report the results obtained by numerical simulations using the proposed model. The following parameters have been used in Algorithm 3: , , . For the line search, the range for the step size was . For the initial guess, we used , . For the 2-D layered medium, the grid size was set to with square voxels of size 1 (mm), i.e., the medium is , and (mm). The values of the extinction coefficients are set between 1.05 and 1.55 (), and the upper bound in Eq. (30) is set to (). The parameter of the Gaussian phase function is 0.2 or 0.4, and the scattering coefficient is set to (). The threshold for excluding low contribution paths is . The ground truth and the estimated extinction coefficients are shown in Fig. 7. The matrix plots in the top row of the figure represent five different media [from (a) to (e)] used for the simulation. Each voxel is shaded in gray according to the values of the extinction coefficient , and darker gray represents larger values of . Also, the values of are displayed at each voxel. In the same manner, the middle and bottom rows show the estimated results when the following values of the parameter of the Gaussian phase function were used: and 0.4. Figure 8 shows the observations in a matrix form, from which the extinction coefficients are estimated. Each element in these plots is now an observation . We can see observations with higher values (shown in darker shades of gray in the plots) on the diagonal. The observations obtained for seem to be fainter than those obtained for due to the larger amount of scattering. Fig. 7Numerical simulation results for a grid of size . Darker shades of gray represent larger values (more light is absorbed at the voxel). The bars on the side show extinction coefficient values [] in gray scale. The first row shows ground truth for five different types of media [(a)–(e)] used for the simulation. The second and third rows show estimated results for and , respectively, of the Gaussian phase function. 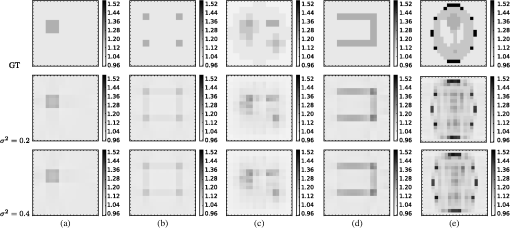 Fig. 8Visualization of the observations in a matrix form. Each matrix shows in its ’th row and ’th column. The horizontal index indicates the location of the light source, and the vertical index indicates the location of the detector. Hence, is the light intensity with the detector at and the light source at . Darker shades of gray represent larger observation values (brighter light is observed). Left to right columns: five different media [(a)–(e)] used for the simulation in the same order as in Fig. 7. Top to bottom rows: for T2B and L2R configurations for and .  The left-most column of Fig. 7(a) shows the simplest case: the medium has almost homogeneous extinction coefficients of value 1.05 (voxels shaded in light gray) except for a few voxels with much higher coefficients of 1.2 (voxels shaded in dark gray), which means that those voxels absorb much more light than other voxels. The coefficients are estimated reasonably well as shown in the middle and bottom rows, and the root mean squared error (RMSE) shown in Table 1 is small enough with a relative error of to the background coefficient value. The other media, shown in columns (b) to (e), have more complex distributions of the extinction coefficients. We summarize the quality of the estimated results in terms of RMSE in Table 1. Numbers in the brackets are relative errors of RMSE to the background extinction coefficient values (i.e., 1.05). Computation time is also shown in Table 1. Note that our proposed method has been currently implemented in MATLAB®, which can be accelerated further by using C++. Table 1Root mean squared errors (RMSEs) and computation time for the numerical simulations for five different types of media [(a) to (e)] with a grid size of 20×20, for two different Gaussian phase function parameter values. Numbers in the brackets are relative errors of RMSE to the background extinction coefficient values (i.e., 1.05).
The values of the cost function over iterations of the outer loop in Algorithm 3 are shown in Fig. 9 for each medium. These curves show that the proposed method effectively minimizes the original objective function [Eq. (31)] for the five different types of media shown here and probably for other media. Figure 10 demonstrates how the log-barriered cost function in Algorithm 3 evolves over all iterations of the inner loop; the number of iterations in the horizontal axis accumulates all inner iterations of the Quasi-Newton method. We can see that each inner loop successively minimizes the log-barriered function and the warm start (reusing the Hessian from the previous outer loop) may help the gap of values between inner loops. Fig. 9Original cost function values over iterations of the outer loop of Algorithm 3 with (a) and (b) 0.4. The horizontal axis shows the number of outer iterations, and the vertical axis represents the log of the original cost function values. Different plots indicate five different types of media [(a)–(e)] used for the simulation. 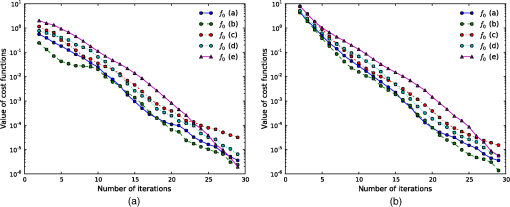 Fig. 10Log-barriered cost function values over iterations of all inner loops of Algorithm 3 for medium (e) with [(a) and (b)] and 0.4 [(c) and (d)]. The horizontal axis shows the number of total inner iterations accumulated across different outer loops. The vertical axis represents the original cost function values (left) in log scale and (right) in linear scale. 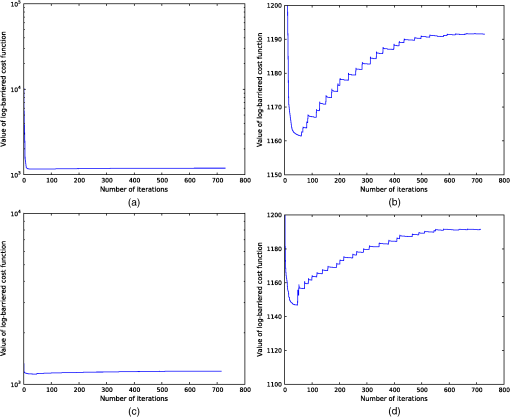 5.1.Comparison ResultsWe compare our method to a standard DOT with FEM (Refs. 64 and 65) using different optimization methods implemented in the Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software (EIDORS).64,65 The ground truth used in this comparison is shown in the top row of Figs. 11(a)–11(e): medium of size with extinction coefficient distributions almost the same as those shown in Figs. 7(a)–7(e). Fig. 11Numerical simulation results for a grid of size , comparing our method to diffuse optical tomography (DOT) with two solvers. Darker shades of gray represent larger values (more light is absorbed at the voxel). The bars on the side show extinction coefficient values [] in gray scale. First row shows the ground truth for five different types of media [(a)–(e)] used for the simulation. Second row shows the estimated results of the proposed method. Third and fourth rows show estimated results for DOT by using Gauss-Newton (GN) and primal-dual (PD) interior point solvers.  For solving DOT by EIDORS, we used triangle meshes (i.e., each voxel is divided into two triangle meshes), and for the boundary condition, we placed 16 light sources and 16 detectors at the same intervals around the medium. We chose two solvers: Gauss-Newton (GN) method and primal-dual (PD) interior point method. We used as the initial guess for both our method and EIDORS. The results obtained by our method () and DOT with GN and PD are shown in Fig. 11. The results obtained by the proposed method are shown in the second row, which are similar to those in the third row of Fig. 7. The third row in Fig. 11 shows the results for DOT with GN. These kind of blurred results are typical for DOT estimation due to its diffusion approximation. The last row shows results for DOT with PD, which look better than those obtained for DOT with GN, but still have a tendency of overestimating the high coefficient value areas. We summarize RMSE values and computation time for each method in Table 2 in the same format as Table 1. RMSE values of our method are two to five times smaller than those of DOT, and this demonstrates that the proposed method can achieve much more accurate results. The current disadvantage is its large computation cost, as our method takes up to 1000 times longer than DOT. We plan to reduce the computation cost by optimizing the code using C++ and adopting other solvers. Table 2RMSEs and computation time for the numerical simulations for five different types of media [(a) to (e)] with grid size of 24×24, for the proposed method and diffuse optical tomography (DOT) with two solvers. Numbers in the brackets are relative errors of RMSE to the background extinction coefficient values (i.e., 1.05).
6.Conclusion with DiscussionIn this paper, we have proposed a path integral based approach to optical tomography for multiple scattering in discretized participating media. Assuming the scattering coefficients and phase function are known and uniform, the extinction coefficients at each voxel in a 2-D layered medium are estimated by using an interior point method. Numerical simulation examples are shown to demonstrate that the proposed framework works better than DOT in the simplified experimental setup, while its computation cost needs to be reduced. There are many directions for further research, including relaxing the assumption of 2-D layered scattering model to more realistic scattering with other phase functions, using paths generated by Monte Carlo based statistical methods, extending the formulation to a full 3-D scattering model, and solving the issues mentioned below. Limitations—stability and uniqueness: The current formulation presented in this paper estimates only the extinction coefficients; the scattering coefficients and phase function parameters are assumed to be known and uniform. This is one of the limitations of the proposed method, however, it is a common limitation of optical tomography. It is known that the scattering and absorption coefficients cannot be separated from stationary measurements of light intensity,34 and the solutions are not unique. Also, given stationary measurements without angle information, the problem becomes ill-posed6,7 and hence not stable. To overcome this limitation, we need to extend the current formulation to handle other measurements that enable stability and uniqueness, such as time-dependent, frequency-dependent, or angle-dependent measurements. Computational cost: A large part of the computational cost of the proposed method comes from the forward model prediction [Eq. (28)], which appears in the gradient computation [Eq. (7)]. It depends on the number of paths ; we currently use about 700 paths out of all possible paths, and for each path, we need to compute path vectors , , and factors . A possible acceleration is the precomputation of these variables, but this would lead to a trade-off with storage cost. Each has dimensions of , each pair of has about 700 vectors of , and the number of pairs (hence observations) is . In total, memory would be required even if single precision floating numbers were used for storing all . Fortunately, these vectors are necessarily sparse, and we have used sparse matrices to store them. However, the increase will be linear in the number of paths and quadratic with the grid size . Therefore, we plan to consider more efficient implementations. AcknowledgmentsThis research is supported in part by a grant from the Japan Society for the Promotion of Science (JSPS) through the Funding Program for Next Generation World-Leading Researchers (NEXT Program) initiated by the Council for Science and Technology Policy (CSTP), and by JSPS KAKENHI Grant Number 26280061. ReferencesS. R. Arridge and M. Schweiger,
“Image reconstruction in optical tomography,”
Philos. Trans. R. Soc. B, 352
(1354), 717
–726
(1997). http://dx.doi.org/10.1098/rstb.1997.0054 Google Scholar
S. R. Arridge and J. C. Hebden,
“Optical imaging in medicine: II. Modelling and reconstruction,”
Phys. Med. Biol., 42
(5), 841
(1997). http://dx.doi.org/10.1088/0031-9155/42/5/008 Google Scholar
J. C. Hebden, S. R. Arridge and D. T. Delpy,
“Optical imaging in medicine: I. Experimental techniques,”
Phys. Med. Biol., 42
(5), 825
(1997). http://dx.doi.org/10.1088/0031-9155/42/5/007 Google Scholar
S. R. Arridge,
“Optical tomography in medical imaging,”
Inverse Probl., 15 R41
–93
(1999). http://dx.doi.org/10.1088/0266-5611/15/2/022 INPEEY 0266-5611 Google Scholar
S. R. Arridge and J. C. Schotland,
“Optical tomography: forward and inverse problems,”
Inverse Probl., 25
(12), 123010
(2009). http://dx.doi.org/10.1088/0266-5611/25/12/123010 INPEEY 0266-5611 Google Scholar
G. Bal,
“Inverse transport theory and applications,”
Inverse Probl., 25
(5), 053001
(2009). http://dx.doi.org/10.1088/0266-5611/25/5/053001 INPEEY 0266-5611 Google Scholar
K. Ren,
“Recent developments in numerical techniques for transport-based medical imaging methods,”
Commun. Comput. Phys., 8 1
–50
(2010). http://dx.doi.org/10.4208/cicp.220509.200110a Google Scholar
A. Charette, J. Boulanger and H. K. Kim,
“An overview on recent radiation transport algorithm development for optical tomography imaging,”
J. Quant. Spectrosc. Radiat. Transf., 109
(17–18), 2743
–2766
(2008). http://dx.doi.org/10.1016/j.jqsrt.2008.06.007 Google Scholar
A. A. Kokhanovsky, Light Scattering Media Optics: Problems and Solutions, 3rd ed.Springer, New York
(2004). Google Scholar
H. W. Jensen, Realistic Image Synthesis Using Photon Mapping, AK Peters, Ltd., Natick, MA
(2001). Google Scholar
J. T. Kajiya,
“The rendering equation,”
SIGGRAPH Comput. Graph., 20 143
–150
(1986). http://dx.doi.org/10.1145/15886.15902 CGRADI 0097-8930 Google Scholar
M. Pharr and G. Humphreys, Physically Based Rendering: From Theory to Implementation, 2nd ed.Morgan Kaufmann, San Francisco, CA
(2010). Google Scholar
E. Cerezo et al.,
“A survey on participating media rendering techniques,”
Vis. Comput., 21
(5), 303
–328
(2005). http://dx.doi.org/10.1007/s00371-005-0287-1 VICOE5 0178-2789 Google Scholar
N. Kurachi, The Magic of Computer Graphics, A. K. Peters, Ltd., Natick, MA
(2011). Google Scholar
R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York
(1965). Google Scholar
J. Tessendorf,
“Radiative transfer as a sum over paths,”
Phys. Rev. A, 35
(2), 872
–878
(1987). http://dx.doi.org/10.1103/PhysRevA.35.872 Google Scholar
M. Pauly, T. Kollig and A. Keller,
“Metropolis light transport for participating media,”
in Proc. of the Eurographics Workshop on Rendering Techniques,
11
–22
(2000). Google Scholar
E. Veach and L. J. Guibas,
“Metropolis light transport,”
in Proc. of the 24th Annual Conf. on Computer Graphics and Interactive Techniques,
65
–76
(1997). Google Scholar
E. P. Lafortune and Y. D. Willems,
“Rendering participating media with bidirectional path tracing,”
in Proc. of the Eurographics Workshop on Rendering Techniques,
91
–100
(1996). Google Scholar
E. Veach,
“Robust Monte Carlo methods for light transport simulation,”
Stanford University,
(1997). Google Scholar
W. Jarosz,
“Efficient Monte Carlo methods for light transport in scattering media,”
University of California, San Diego,
(2008). Google Scholar
B. Segovia,
“Interactive light transport with virtual point lights,”
Université Lyon 1,
(2007). Google Scholar
A. W. Kristensen,
“Efficient unbiased rendering using enlightened local path sampling,”
Technical University of Denmark,
(2011). Google Scholar
M. L. Adams and E. W. Larsen,
“Fast iterative methods for discrete-ordinates particle transport calculations,”
Prog. Nucl. Energy, 40
(1), 3
–159
(2002). http://dx.doi.org/10.1016/S0149-1970(01)00023-3 Google Scholar
K. Ren, G. Bal and A. H. Hielscher,
“Frequency domain optical tomography based on the equation of radiative transfer,”
SIAM J. Sci. Comput., 28 1463
–1489
(2006). http://dx.doi.org/10.1137/040619193 SJOCE3 1064-8275 Google Scholar
S. Boyd and L. Vandenberghe, Convex Optimization, Cambridge University Press, Cambridge
(2004). Google Scholar
T. Tamaki et al.,
“Multiple-scattering optical tomography with layered material,”
in Int. Conf. on Signal-Image Technology Internet-Based Systems,
93
–99
(2013). Google Scholar
B. Yuan et al.,
“Layered optical tomography of multiple scattering media with combined constraint optimization,”
in 21st Japan-Korea Joint Workshop on Frontiers of Computer Vision,
1
–6
(2015). Google Scholar
N. J. McCormíck,
“Recent developments in inverse scattering transport methods,”
Transp. Theory Stat. Phys., 13
(1–2), 15
–28
(1984). http://dx.doi.org/10.1080/00411458408211649 Google Scholar
L. Florescu, V. A. Markel and J. C. Schotland,
“Single-scattering optical tomography: simultaneous reconstruction of scattering and absorption,”
Phys. Rev. E, 81 016602
(2010). http://dx.doi.org/10.1103/PhysRevE.81.016602 Google Scholar
L. Florescu, J. C. Schotland and V. A. Markel,
“Single-scattering optical tomography,”
Phys. Rev. E, 79 036607
(2009). http://dx.doi.org/10.1103/PhysRevE.79.036607 Google Scholar
M. Schweiger, A. Gibson and S. R. Arridge,
“Computational aspects of diffuse optical tomography,”
Comput. Sci. Eng., 5
(6), 33
–41
(2003). http://dx.doi.org/10.1109/MCISE.2003.1238702 Google Scholar
D. A. Boas et al.,
“Imaging the body with diffuse optical tomography,”
IEEE Signal Process. Mag., 18
(6), 57
–75
(2001). http://dx.doi.org/10.1109/79.962278 Google Scholar
A. P. Gibson, J. C. Hebden and S. R. Arridge,
“Recent advances in diffuse optical imaging,”
Phys. Med. Biol., 50 R1
–R43
(2005). http://dx.doi.org/10.1088/0031-9155/50/4/R01 PHMBA7 0031-9155 Google Scholar
L. G. Henyey and J. L. Greenstein,
“Diffuse radiation in the galaxy,”
Astrophys. J., 93 70
–83
(1941). http://dx.doi.org/10.1086/144246 Google Scholar
P. Blasi, B. Saec and C. Schlick,
“A rendering algorithm for discrete volume density objects,”
Comput. Graph. Forum, 12
(3), 201
–210 1993). Google Scholar
W. M. Cornette and J. G. Shanks,
“Physically reasonable analytic expression for the single-scattering phase function,”
Appl. Opt., 31 3152
–3160
(1992). http://dx.doi.org/10.1364/AO.31.003152 APOPAI 0003-6935 Google Scholar
T. Nishita et al.,
“Display of the earth taking into account atmospheric scattering,”
in Proc. of the 20th Annual Conf. on Computer Graphics and Interactive Techniques,
175
–182
(1993). Google Scholar
M. Keijzer et al.,
“Light distributions in artery tissue: Monte Carlo simulations for finite-diameter laser beams,”
Lasers Surg. Med., 9
(2), 148
–154
(1989). http://dx.doi.org/10.1002/lsm.1900090210 Google Scholar
P. Edström,
“A two-phase parameter estimation method for radiative transfer problems in paper industry applications,”
Inverse Probl. Sci. Eng., 16
(7), 927
–951
(2008). http://dx.doi.org/10.1080/17415970802080066 INPEEY 0266-5611 Google Scholar
P. Edström,
“Simulation and modeling of light scattering in paper and print applications,”
Light Scattering Reviews 5, 451
–475 Springer Praxis BooksSpringer, Berlin Heidelberg
(2010). Google Scholar
Y. Dobashi et al.,
“An inverse problem approach for automatically adjusting the parameters for rendering clouds using photographs,”
ACM Trans. Graph., 31
(6), 145
(2012). http://dx.doi.org/10.1145/2366145.2366164 Google Scholar
N. Joshi, C. Donner and H. W. Jensen,
“Noninvasive measurement of scattering anisotropy in turbid materials by nonnormal incident illumination,”
Opt. Lett., 31 936
–938
(2006). http://dx.doi.org/10.1364/OL.31.000936 OPLEDP 0146-9592 Google Scholar
M. Baba et al.,
“Estimation of scattering properties of participating media using multiple-scattering renderer,”
in Proc. of the Fourth IIEEJ Int. Workshop on Image Electronics and Visual Computing,
(2014). Google Scholar
I. Gkioulekas et al.,
“Inverse volume rendering with material dictionaries,”
ACM Trans. Graph., 32 162
(2013). http://dx.doi.org/10.1145/2508363.2508377 ATGRDF 0730-0301 Google Scholar
V. S. Antyufeev, Monte Carlo Method for Solving Inverse Problems of Radiation Transfer, VSP Intl. Science, The Netherlands
(2000). Google Scholar
G. I. Marchuk et al., The Monte Carlo Methods in Atmospheric Optics, 54
–146 Springer, Berlin Heidelberg
(1980). Google Scholar
P. Edström,
“A fast and stable solution method for the radiative transfer problem,”
SIAM Rev., 47
(3), 447
–468
(2005). http://dx.doi.org/10.1137/S0036144503438718 SIREAD 0036-1445 Google Scholar
C. K. Hayakawa, J. Spanier and V. Venugopalan,
“Coupled forward-adjoint Monte Carlo simulations of radiative transport for the study of optical probe design in heterogeneous tissues,”
SIAM J. Appl. Math., 68
(1), 253
–270
(2007). http://dx.doi.org/10.1137/060653111 Google Scholar
C. Hayakawa, J. Spanier, Monte Carlo and Quasi-Monte Carlo Methods 2002, 227
–241 Springer, Berlin Heidelberg
(2004). Google Scholar
Y. Ishii et al.,
“Scattering tomography by Monte Carlo voting,”
in Proc. IAPR International Conference on Machine Vision Applications (MVA2013),
(20132015). http://www.iapr.org/ Google Scholar
R. L. Barbour et al.,
“Model for 3-D optical imaging of tissue,”
1395
–1399
(1990). http://dx.doi.org/10.1109/IGARSS.1990.688761 Google Scholar
M. Raab, D. Seibert and A. Keller,
“Unbiased global illumination with participating media,”
in Monte Carlo and Quasi-Monte Carlo Methods,
591
–605
(2008). Google Scholar
S. Premože, M. Ashikhmin and P. Shirley,
“Path integration for light transport in volumes,”
in Proc. of the 14th Eurographics Workshop on Rendering,
52
–63
(2003). Google Scholar
J. Křivánek et al.,
“Unifying points, beams, and paths in volumetric light transport simulation,”
ACM Trans. Graph., 33
(103), 1
–13
(2014). http://dx.doi.org/10.1145/2601097.2601219 ATGRDF 0730-0301 Google Scholar
S. L. Jacques and X. Wang,
“Path integral description of light transport in tissues,”
Proc. SPIE, 2979 488
–499
(1997). http://dx.doi.org/10.1117/12.280283 PSISDG 0277-786X Google Scholar
M. J. Wilson and R. K. Wang,
“A path-integral model of light scattered by turbid media,”
J. Phys. B, 34
(8), 1453
(2001). http://dx.doi.org/10.1088/0953-4075/34/8/310 Google Scholar
J. C. Schotland,
“Tomography with diffusing photons: a Feynman path integral perspective,”
in Proc. of IEEE Int. Conf. on Acoustics, Speech, and Signal Processing,
3791
–3794
(2000). Google Scholar
J. C. Schotland,
“Path integrals and optical tomography,”
Contemp. Math., 548 77
–84
(2011). Google Scholar
P. Dutre et al., Advanced Global Illumination, 2nd ed.A K Peters/CRC Press, Boca Raton, FL
(2003). Google Scholar
V. S. Antyufeev,
“On the distribution of a random variable,”
Sib. Zh. Ind. Mat., 15
(2), 3
–10
(2012). Google Scholar
J. Heino et al.,
“Anisotropic effects in highly scattering media,”
Phys. Rev. E, 68 031908
(2003). http://dx.doi.org/10.1103/PhysRevE.68.031908 Google Scholar
J. Nocedal and S. J. Wright, Numerical Optimization, 2nd ed.Springer, New York
(2006). Google Scholar
N. Polydorides,
“Image reconstruction algorithms for soft-field tomography,”
University of Manchester: UMIST,
(2002). Google Scholar
N. Polydorides and W. R. Lionheart,
“A MATLAB toolkit for three-dimensional electrical impedance tomography: a contribution to the electrical impedance and diffuse optical reconstruction software project,”
Meas. Sci. Technol., 13
(12), 1871
(2002). http://dx.doi.org/10.1088/0957-0233/13/12/310 Google Scholar
BiographyBingzhi Yuan received his BE degree in software engineering from the Beijing University of Posts and Telecommunications, China, and his ME degree in engineering from Hiroshima University, Japan, in 2010 and 2013, respectively. Currently, he is a PhD student at Hiroshima University. Toru Tamaki received his BE, ME, and PhD degrees in information engineering from Nagoya University, Japan, in 1996, 1998, and 2001, respectively. After being an assistant professor at Niigata University, Japan, from 2001 to 2005, he is currently an associate professor in the Department of Information Engineering, Graduate School of Engineering, Hiroshima University, Japan. His research interests include computer vision and image recognition. Yasuhiro Mukaigawa received his ME and PhD degrees from the University of Tsukuba in 1994 and 1997, respectively. He became a research associate at Okayama University in 1997, an assistant professor at the University of Tsukuba in 2003, an associate professor at Osaka University in 2004, and a professor at Nara Institute of Science and Technology (NAIST) in 2014. His current research interests include photometric analysis and computational photography. Hiroyuki Kubo received his ME and PhD degrees from Waseda University in 2008 and 2012. Since 2014, he has been an assistant professor at NAIST, Japan. Bisser Raytchev received his PhD in informatics from Tsukuba University, Japan, in 2000. After being a research associate at NTT Communication Science Labs and AIST, he is presently an assistant professor in the Department of Information Engineering, Hiroshima University, Japan. His current research interests include computer vision, pattern recognition, high-dimensional data analysis, and image processing. Kazufumi Kaneda is a professor in the Department of Information Engineering at Hiroshima University. He received his BE, ME, and DE degrees from Hiroshima University, Japan, in 1982, 1984, and 1991, respectively. In 1986, he joined Hiroshima University. He was a visiting researcher at Brigham Young University from 1991 to 1992. His research interests include computer graphics and scientific visualization. |


