|
|
1.IntroductionMorphometric measures of brain structures can be useful in determining changes related to diverse pathologies. Attempts have been made to characterize brain shape using different metrics, but this continues to be an open challenge. A great variety of diseases can affect brain morphology either globally or in some specific regions. Such is the case of Alzheimer’s disease (AD) which is a neurodegenerative condition characterized by progressive cognitive deterioration that limits the performance of daily activities. Its diagnosis is based on the information provided by a careful clinical examination, a thorough interview of the patient and relatives, imaging, and a neuropsychological assessment.1 A transitional stage prior to AD is known as the mild cognitive impairment (MCI) stage,2 which is characterized by memory loss with cognitive disorder. Studies have reported that between 10% and 64% of subjects with MCI are at risk of developing AD. This latter pathology develops primarily in subjects aged 65 and older and affects approximately 25 million people worldwide.1 The timely detection of changes in brain tissue caused by MCI could prompt actions aimed at preventing or delaying the progression of the disease, either from normal subjects to MCI or from MCI to AD. A decline in memory, loss of attention, and lack of ability to perform daily activities indicate a high probability of having dementia; subjects with these symptoms are usually evaluated with neuropsychological standardized tests.3,4 Currently, an expert diagnosis is based on the use of brain magnetic resonance imaging (MRI), which is a noninvasive technique that allows the observation of the morphometric changes caused by AD; these studies evidence a loss of volume in the cerebral cortex, a ventricular dilation, and a cerebral deformation, mainly affecting the temporal and parietal lobes.5,6 At substructure level, researchers report4,7,8 that AD has a prevalence in fronto-temporal degeneration, atrophying hippocampus, and amygdala tissue. With early detection of these pathologies, action can be taken in order to delay the neurodegenerative process; therefore, it is important to have indices that help to describe and characterize these pathologies, in addition to automated methods that support their diagnosis. Several studies report the use of volume measurements to describe the changes related to AD,4,8–12 finding significant differences in gray matter (GM) volume between healthy controls (HC) and MCI compared with AD. Normalized volumes (NVs) of GM have been reported in Ref. 11: 0.36 for HC, 0.345 to 0.355 for MCI, and 0.34 for AD subjects. Other authors13 have found a loss of GM tissue in the temporal lobe of about 12% between HC and AD and 8% between MCI and AD. Other researchers have found that this neurodegenerative process causes an asymmetry in the cerebral hemispheres,11 which increases as AD progresses. Most of the studies rely on volume indices to quantify brain changes during aging. A preliminary study carried out by our research group proposed the discrete compactness (DC) to measure brain shapes in normal synthetic MR structures; we obtained a mean absolute volume of and mean compactness of 0.876 for GM and a mean absolute volume and 0.917 mean compactness for white matter (WM); this research aimed to explore the compactness as a shape index to describe brain structures.14 The use of image processing techniques and biomarkers that describe the morphology and geometry of normal and pathological brain structures is useful to automate the diagnosis. Some researchers15 have used brain MRI studies to obtain geometric biomarkers, such as gray and WM volumes, enclosing surface area, circularity, elongation, and rectangularity of different structures. These features together with a principal component analysis and a combination of support vector machine (SVM) and self-organizing maps are used to classify normal and demential subjects, obtaining a classification rate of 94.12% between HC and AD and 88.89% between HC and MCI. Chincarini et al.16 used an automatic selection of features obtained from substructures, such as the hippocampus, amygdala, insula, and middle and inferior temporal gyri, together with a classification scheme based on SVM, obtaining an area under the curve (AUC) of 0.97 between HC and AD. In the present study, we propose the use of an optimized DC measure and the NV to describe, characterize, and differentiate the morphology of brain structures in three populations: HC, MCI, and AD, matched by age in a 68 to 85 years rank. The purpose was to explore and compare the capability of these two parameters to differentiate brain structures that are affected by the pathological processes of aging and to determine the compactness sensitivity to morphological changes. Additionally, the convenience of incorporating a shape measure based on the three-dimensional (3-D) DC is demonstrated; these parameters, when used within an optimized classification model, together with properly selected features, provide an adequate means of determining different stages of normal and abnormal aging. 2.Methodology2.1.Studied PopulationsThree groups were analyzed: normal HC, subjects presenting MCI, and patients with AD. Thirty volumes of brain MRI were selected for each class from the Alzheimer’s disease neuroimaging initiative (ADNI) database;17 health condition was determined within the database using the Mini-Mental State Examination score, with ranges 28–30 for HC, 25–27 for MCI, and 21–25 for AD. The three populations were paired by age, between 68 and 85 years. Images were obtained with 1.5T and 3T systems following a T1 protocol and were in some cases interpolated with a cubic function to achieve a isotropic sampling resolution. 2.2.SegmentationBrain images were globally segmented to extract three main structures: GM, WM, and cerebrospinal fluid (CSF), using a nonparametric technique of probability density function estimation, based on the mean-shift algorithm.18 The procedure begins by filtering the data with a modified mean-shift method that incorporates edge-confidence maps, in order to obtain the distribution modes without any a priori information. Afterward, an adjacency graph is constructed and analyzed to fuse those regions belonging to the same class, given spatial and intensity similarity measures; a final step is applied to prune regions whose size is below a certain threshold, assigning them to the nearest class. Brain tissues’ classification is carried out by considering anatomical atlases with the Statistical Probability Mapping (SPM) software.19 The outcome of this procedure is a set of images, where GM, WM, and CSF are segmented and from these we construct the global anatomical volumes that will be measured using compactness indices. Also, a more detailed separation of these structures is accomplished by using the Individual Brain Atlases using Statistical Parametric Mapping (IBASPM),20,21 that uses templates containing those substructures belonging to the frontal, temporal, parietal, and occipital lobes. These templates are registered to the same data space and applied to delimit the substructures corresponding, for both hemispheres, to frontal (FR, FL), temporal (TR, TL), parietal (PR, PL), and occipital (OR, OL) lobes. These regions, together with WM and GM, give a total of 10 brain structures to be characterized. 2.3.FeaturesThe classical compactness measure for a 3-D object is defined from the enclosing surface area and the volume with the following ratio: ; it is a normalized dimensionless measure, minimized by a sphere. This compactness measure is easy to compute for 3-D shapes, but is very sensitive to a noisy perimeter or enclosing area.22 The 3-D DC23,24 is a more robust measure, because it is more dependent on the object’s interior than on its external characteristics. It considers the surface area of those voxels that make contact in 3-D; it varies between 0 and 1 and is defined for 3-D shapes as where is the number of voxels and is the enclosing surface of the object. In this case, maximal compactness is one and corresponds to a cube, whereas minimal compactness is zero and corresponds to an object having all its voxels disjoint. Figure 1 shows the example of an object with different shapes but with the same number of voxels. The variation of its compactness measure can be appreciated as the object “spreads” spatially; the decrease of compactness can be observed from (a) to (d), demonstrating the measure’s sensitivity to the object’s deformation.Fig. 1Example of the three-dimensional (3-D) discrete compactness (DC) measure on a synthetic shape that is gradually disagregated [(a) to (d)], while keeping the same number of voxels.  The compactness measure has the following properties:
This index was employed to globally and locally characterize and differentiate brain structures in healthy subjects and in patients with some pathology affecting brain morphology. For this application, translation and rotation invariances are important to represent the brain shape in a population, where subject positioning can vary during image acquisition. Also, scale invariance and index normality are useful properties, because the comparison of compactness of brain tissue in different subjects can be carried out, regardless of size but not of shape. Additionally, the NV was obtained for each structure; this measure has been widely used in the literature to determine size changes during aging; it is computed as the ratio of the volume of a given brain structure to the total intracranial volume.25 2.4.Classification and Feature SelectionSVMs are used in pattern recognition in a great number of applications due to their robustness and learning ability from experimental data.26 SVM separates a given set of binary-labeled training data by means of a feature-space hyperplane that is maximally distant from the training samples of the two classes. Details of this classification model can be found elsewhere.27–29 Three SVM classifiers with Gaussian kernel were designed using the publicly available libSVM library,30 optimized for pairwise classification of the three populations: HC versus MCI, MCI versus AD, and HC versus AD, using fivefold cross-validation. Misclassification cost and kernel width gamma for the SVMs were selected by the grid-search method. For each class pair, SVMs were constructed independently from the 10 NV and the 10 DC features. Additionally, a sequential forward selection (SFS) algorithm31 seeking to maximize the classification rate was used to obtain optimal feature subsets for NV, DC, and combined NV + DC measures. For the three trained SVMs, expected performance () was determined by computing classification accuracy [percent correct (PC)] and AUC from a fivefold cross-validation run. 3.Results3.1.Descriptive Statistics of IndicesThree segmented brains corresponding to one representative example for each analyzed group are shown in Fig. 2. The intracranial volume was determined by adding the three segmented volumes (GM, WM, and CSF) and yielded for HC, for MCI, and for AD. The 3-D reconstructions (right column in Fig. 2) correspond to GM, and the associated DC and NV values are also indicated. The decrease of volume that appears from normal to AD subjects can be observed both visually and quantitatively, together with a corresponding decline of the compactness measure. Fig. 2MRI segmentations for HC (a), MCI (b), and AD (c) subjects. For each section, first row: original slices; second row: gray matter (GM) (in gray) and white matter (WM) (in white) segmented regions; right column: GM 3-D reconstructions with their corresponding DC and NV measures. 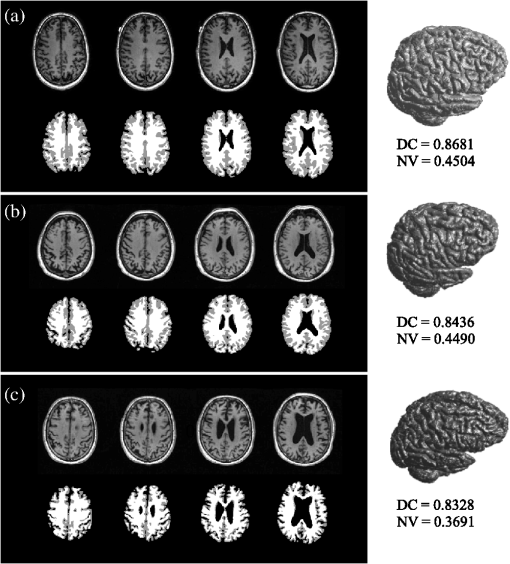 Table 1 shows the NV and DC measures for all the segmented regions (to facilitate the data presentation, all measures were scaled by a factor of 1000). Each column displays the measured indices for each population. Asterisks (*) indicate the significant differences between the group and AD, whereas crosses (+) specify the differences with respect to the MCI population. Table 1Distribution of image features for both populations under study (mean±standard deviation×1000).
Note: Abbreviations: HC, healthy controls; MCI, mild cognitive impairment; and AD, Alzheimer’s disease; GM, gray matter; WM, white matter; FR, frontal right; FL, forntal left; OR, occipital right; OL, occipital left; TR, temporal right; TL, temporal left; PR, parietal right; PL, parietal left.Group comparisons using ANOVA and Tukey statistical tests at significance level (p<0.05).* indicates the significant differences compared with the AD group+ indicates the significant differences compared with the MCI group. 3.2.Classification Power of IndicesThe areas under the ROC curves for individual indices, measured to discriminate between populations, are shown in Table 2. The rows indicate all the segmented structures, whereas the columns indicate the comparison of populations by pairs: the first three correspond to the NV measurements and the last three to the DC indices. Table 2Area under ROC curves (AUC) measuring the discrimination capability of individual indices among segmented regions.
Three classifiers were designed for pairwise separation between populations. The estimated classification performance is reported in Table 3 (first row: HC versus MCI; second row: HC versus AD; third row MCI versus AD) in terms of PC and AUC (). Columns show these measures for classifiers built from different feature sets: NV only, DC only, and combined NV + DC. In the first two cases, performance for the full feature set (FFS) and the optimal feature set (OFS) is shown; in the last case, only OFS results are presented, since the use of the 20 features altogether provides poor classification. Optimal feature sets are shown in Table 4, as obtained from the SFS algorithm for each classifier. Columns indicate whether a feature from the full set was selected or not in each case. Table 3Support vector machine (SVM) classification performance, reported as AUC and percent correct (PC) in each row. Columns correspond to classifiers using NV, DC, and combined NV + DC features. FFS: full feature set; OFS: optimized feature set.
Table 4Optimal features selected with SFS for each classifier case.
Note: “x” indicates that the NV feature for the corresponding region was selected; “o” indicates that the DC feature for the corresponding region was selected; “-” indicates that the feature was not selected. 4.DiscussionThe main contribution of this work consists of the introduction of a 3-D morphological descriptor (the DC), beyond the standard use of volume measures that significantly improves the aging stage classification from segmented MRI volumes. As a first step, we observed that the mean intracranial volume obtained for HC, MCI, and AD populations did not show statistically significant differences according to the ANOVA test; this may be due to the high variability of the populations in terms of size and weight. Heckemann et al.11 found a stable intracranial volume for the three groups, although with some differences between MCI and AD populations; they recommend the normalization of brain volumes to reduce size and gender intragroup variations. Therefore, in this work, all volumes were normalized. When the segmentation of structures in the studied populations was carried out, a gradual change in size and shape of GM and WM is observed, as the aging process increases (Fig. 2); the deformation caused by the pathology was also observed in the segmentation of the four lobes: frontal, occipital, parietal, and temporal. Although the applied segmentation method has been thoroughly validated for normal brain MRI, obtaining high similarity indices with respect to manual segmentations,18 it has yet to be validated in abnormal brains. In order to test the separation capability between the three studied populations, the DC index was compared with NV. First, a global analysis considering only GM and WM was performed; when applying ANOVA and Tukey tests between populations (HC, MCI, and AD), a slightly different behavior between the two indices (Table 1) can be observed: NV and DC indices for GM are only different between HC versus AD and MCI versus AD. Our results are consistent with those found and reported by Heckemann et al.,11 relative to the NV parameter. With respect to the measurements made in WM, statistical differences were found in HC versus AD and MCI versus AD comparisons (Table 1); the consistency of the compactness index for the three populations and their small variance ( to ) can be noticed. Moreover, the studies found in the literature7,11 reported an increase in the volume of the cerebral ventricles, which in turn causes changes in the WM volume and shape. However, these results should be taken with caution, as several authors reported a significant change in the intensity of WM observed with the MR technique,8,11 due to the normal or pathological aging process. On the other hand, several studies report the differences in lobes NV between the groups of HC, MCI, and AD;11 in a more detailed analysis, a reduction in substructures, such as the amygdala and the middle and inferior temporal gyri, and ventricular dilation affecting the temporal area are also reported. Liu et al.4 reported that the main differences are found in the ventricular system, hippocampus, amygdala, and entorhinal cortex; the latter are the temporal lobe subregions. This is clear evidence that the most affected structure by AD is the temporal lobe, which is consistent with the results reported in Table 1. We can observe significant differences between HC and AD in the temporal and left parietal lobes, whereas between HC and MCI the only differences found are in the left parietal lobe. When the statistical tests were carried out, we observed significant differences between HC, MCI, and AD subjects in the temporal and parietal lobes; this supports the sensitivity of the compactness indices to morphological changes in these lobes. On the other hand, the frontal and occipital lobes only presented differences between HC versus AD and MCI versus AD, which suggests that the compactness measure can discriminate these groups. Some researches report that the volume changes of the amygdala can vary between 14% and 44% and this can be useful as an AD predictor.4 Other author8 indicate that the hypothalamus is the most affected region in AD and that, by combining a manual volume segmentation of the hypothalamus with the volume of other structures, a sensitivity of up to 90% and a specificity of up to 94% can be attained. This leads to classification rates ranging between 80% and 90% for the separation of HC and AD populations. With the purpose of showing the real discrimination capability of the measured indices to separate the three studied populations, the sensitivity and specificity were determined for each index and the ROC curves were obtained for all structures; the corresponding areas under the ROC curves are shown in Table 2. It is convenient to recall that an AUC of 0.5 represents a random selection and a poor discriminative power, while a unitary AUC corresponds to an excellent class separation. For the classification between HC and MCI groups, none of the NV show a good separation, it being the AUC of the GM with the highest value (0.69). The corresponding DCs (column 4 of Table 2) show that GM, TR, TL, and PL could be good representative structures to highlight changes () between HC and MCI subjects. The classification capability of NV and DC is higher when discriminating between HC and AD in global GM and WM analyses. The tested indices seem to provide a better selection power between these two populations and this is corroborated by the AUCs that are above 0.8 (first and second rows in Table 2). In particular, it is remarkable that the DC of WM and GM has AUCs that exceed the threshold of 0.9, which is much higher than that of the NV AUCs. With respect to the lobes’ DC indices, AUCs of up to 0.95 for both left and right temporal lobes were obtained. AUCs of 0.93 and 0.91 for the amygdala and the medial temporal gyrus, respectively, by contrasting HC with AD have been reported elsewhere.16 In the comparison of MCI versus AD (columns 3 and 6 in Table 2), the higher AUCs correspond to global GM and WM. In particular, measures of compactness for these two structures have a higher AUC (0.82 in GM and 0.91 in WM), as well as the NV for WM, which has an AUC of 0.9. At the lobe level, it can be seen that the compactness index is a better discriminator than the volume measure, showing an AUC of 0.81 for the left frontal lobe and 0.79 for the left temporal and occipital lobes. In the study published by Chincarini et al.,16 an AUC of 0.92 is reported, using a classification index composed of several volumetric parameters, for the discrimination between subjects with stable MCI and AD patients. Furthermore, Teipel et al.32 measured the capability of discrimination between these two populations, using as indices of classification the right hippocampus and amygdala volumes, which are structures that show significant changes in the process of pathological aging. These authors reported an AUC for the hippocampal volume of only 0.78 and of 0.65 for the case of the amygdala. These results show that the compactness index can be useful for the selection between populations of HC, MCI, and AD, because it is sensitive to shape changes presented by different brain regions, whereas NV is an indicator that reflects the reduction of tissue, regardless of the shape changes. With these findings, we were able to establish a discrimination strategy that combines an optimized SVM classification model and an optimal selection of features. In Table 3, we can observe that for all features tested, the optimal selection carried out with SFS gives a better classification behavior. On the other hand, DC features better discriminated the three pairwise classifications compared with NVs. The higher performance rates were obtained using NV + DC selected features (last column in Table 3): for HC versus MCI classification, we obtained an 85% accuracy with an AUC of 0.8; previous reports in this case go from 47% to 88%15,33 accuracy and AUCs between 0.73 and 0.92.16,34 These results must be improved, especially because the differentiation of these two aging stages is of particular clinical importance. For the case of HC versus AD classification, our proposed scheme achieves up to 98% accuracy with AUC of 0.97. Previously published works report accuracies in the range of 58% to 94%15,33,35,36 and AUC of 0.9716 with various feature sets and other invasive imaging modalities; therefore, for the separation of these two groups, our proposal outperforms other reported methods. Finally, for the MCI versus AD classification, our best results were 93% accuracy and 0.95 AUC; in contrast, other authors have reported 66% accuracies33 and AUC of 0.79.34 In a recent study, Martínez Torteya et al.37 reported a 96% accuracy when measuring MCI to AD conversion, using several imaging and genetic biomarkers. As can be observed in Table 4, the proposed compactness index is highly relevant for classification purposes. It can also be seen that for all the tested classifiers, the feature selection process includes both the temporal right and left lobes, implying that these structures are useful to discriminate between all groups in accordance with known neurophysiology.8,11,12 5.ConclusionsThe main contribution of this work consists of the introduction of a 3-D morphological descriptor (the DC) beyond the standard use of volume measures that significantly improves the aging stage classification from segmented MRI volumes. Our results show that the proposed compactness index is sensitive to changes in shape but not to an object’s size, so that noticeable differences appear between the mean indices obtained for the studied populations, especially in the temporal lobe. These results suggest that the proposed index can be a reliable complementary parameter to discriminate between normal and abnormal aging processes together with volumetric indices that are commonly used in the clinical environment. The 3-D DC has shown to be relevant for age staging, and increasing performance over volume-based and non-MRI based approaches is reported. This is supported by an adequate selection of a classifier model, which has been thoroughly validated, and the optimal selection of the features being used. Class separation for the MCI and AD groups with the presented method outperforms the previous results, whereas the other group comparisons are similar to those reported elsewhere. Discrimination between these two classes might prove relevant for therapeutic decisions. However, the important discrimination between HC and MCI has yet to be improved. In future work, a combined classifier with multiple outputs must be developed, and other biomarkers considered important for abnormal aging identification must be included in the classification process. AcknowledgmentsThis work was supported by CONACyT (Consejo Nacional de la Ciencia y Tecnología) with scholarship number 35879 for J. L. Perez-Gonzalez. ReferencesR. C. Petersen,
“Mild cognitive impairment as a diagnostic entity,”
J. Intern. Med., 256
(3), 183
–194
(2004). http://dx.doi.org/10.1111/jim.2004.256.issue-3 JINMEO 1365-2796 Google Scholar
D. M. Geslaniet al.,
“Mild cognitive impairment: an operational definition and its conversion rate to Alzheimer’s disease,”
Dementia Geriatr. Cognit. Disord., 19
(5–6), 383
–389
(2005). http://dx.doi.org/10.1159/000084709 DGCDFX 1420-8008 Google Scholar
C. P. Hugheset al.,
“A new clinical scale for the staging of dementia,”
Br. J. Psychiatry, 140
(6), 566
–572
(1982). http://dx.doi.org/10.1192/bjp.140.6.566 BJPYAJ 0007-1250 Google Scholar
Y. Liuet al.,
“Analysis of regional MRI volumes and thicknesses as predictors of conversion from mild cognitive impairment to Alzheimer’s disease,”
Neurobiol. Aging, 31
(5), 1375
–1385
(2010). http://dx.doi.org/10.1016/j.neurobiolaging.2010.01.022 NEAGDO 0197-4580 Google Scholar
M. F. FolsteinS. E. FolsteinP. R. McHugh,
“Mini mental state.” A practical method for grading the cognitive state of patients for the clinician,”
J. Psychiatry Res., 12
(3), 189
–198
(1975). http://dx.doi.org/10.1016/0022-3956(75)90026-6 JPYRA3 0022-3956 Google Scholar
T. N. Tombaugh,
“Trail making test A and B: normative data stratified by age and education,”
Arch. Clin. Neuropsychol., 19
(2), 203
–214
(2004). http://dx.doi.org/10.1016/S0887-6177(03)00039-8 0887-6177 Google Scholar
L. G. ApostolovaP. M. Thompson,
“Mapping progressive brain structural changes in early Alzheimer’s disease and mild cognitive impairment,”
Neuropsychologia, 46
(6), 1597
–1612
(2008). http://dx.doi.org/10.1016/j.neuropsychologia.2007.10.026 NUPSA6 0028-3932 Google Scholar
E. Westmanet al.,
“Multivariate analysis of MRI data for Alzheimer’s disease, mild cognitive impairment and healthy controls,”
NeuroImage, 54
(2), 1178
–1187
(2011). http://dx.doi.org/10.1016/j.neuroimage.2010.08.044 NEIMEF 1053-8119 Google Scholar
S. Maheswaranet al.,
“Longitudinal regional brain volume changes quantified in normal aging and Alzheimer’s APP PS1 mice using MRI,”
Brain Res., 1270 19
–32
(2009). http://dx.doi.org/10.1016/j.brainres.2009.02.045 BRREAP 1385-299X Google Scholar
R. Heckemannet al.,
“A repository of MR morphometry data in Alzheimer’s disease and mild cognitive impairment,”
in Proc. IEEE Int. Symposium on Biomedical Imaging: From Nano to Macro,
875
–878
(2011). Google Scholar
R. A. Heckemannet al.,
“Automatic morphometry in Alzheimer’s disease and mild cognitive impairment,”
NeuroImage, 56
(4), 2024
–2037
(2011). http://dx.doi.org/10.1016/j.neuroimage.2011.03.014 NEIMEF 1053-8119 Google Scholar
G. Karaset al.,
“Global and local gray matter loss in mild cognitive impairment and Alzheimer’s disease,”
NeuroImage, 23
(2), 708
–716
(2004). http://dx.doi.org/10.1016/j.neuroimage.2004.07.006 NEIMEF 1053-8119 Google Scholar
J. Barneset al.,
“Measurements of the amygdala and hippocampus in pathologically confirmed Alzheimer’s disease and frontotemporal lobar degeneration,”
Arch. Neurol., 63
(10), 1434
–1439
(2006). http://dx.doi.org/10.1001/archneur.63.10.1434 ARNEAS 0003-9942 Google Scholar
E. Bribiescaet al.,
“A voxel-based measure of discrete compactness for brain imaging,”
in Proc. 25th Annual lnt. Conf. of the IEEE EMBS,
17
–21
(2003). Google Scholar
Y. Shih-Tinget al.,
“Discrimination between Alzheimer’s disease and mild cognitive impairment using SOM and PSO-SVM,”
Comput. Math. Methods Med., 2013 1
–11
(2013). http://dx.doi.org/10.1155/2013/253670 1748-670X Google Scholar
A. Chincariniet al.,
“Local MRI analysis approach in the diagnosis of early and prodromal Alzheimer’s disease,”
NeuroImage, 58
(2), 469
–480
(2011). http://dx.doi.org/10.1016/j.neuroimage.2011.05.083 NEIMEF 1053-8119 Google Scholar
Alzheimer’s Disease Neuroimaging Initiative (ADNI),
(2012) http://adni.loni.ucla.edu/ ( March ). 2012). Google Scholar
J. R. JimenezV. MedinaO. Yanez,
“Data-driven brain MRI segmentation supported on edge confidence and a priori tissue information,”
IEEE Trans. Med. Imaging, 25
(1), 74
–83
(2006). http://dx.doi.org/10.1109/TMI.2005.860999 ITMID4 0278-0062 Google Scholar
Individual Brain Atlases using Statistical Parametric Mapping (IBASPM),
(2012) http://www.thomaskoenig.ch/Lester/ibaspm.htm ( October ). 2012). Google Scholar
G. Diazet al.,
“Surface area and cortical thickness descriptors reveal different attributes of the structural human brain networks,”
NeuroImage, 50
(4), 1497
–1510
(2010). http://dx.doi.org/10.1016/j.neuroimage.2010.01.028 NEIMEF 1053-8119 Google Scholar
R. Gonzalez, Digital Image Processing, 2nd ed.Prentice Hall, Upper Saddle River, New Jersey
(2002). Google Scholar
E. Bribiesca,
“A measure of compactness for 3D shapes,”
J. Comput. Math. Appl., 40
(10–11), 1275
–1284
(2000). http://dx.doi.org/10.1016/S0898-1221(00)00238-8 JCAMDI 0377-0427 Google Scholar
E. Bribiesca,
“Easy measure of compactness for 2D and 3D shapes,”
Pattern Recognit., 41
(2), 543
–554
(2008). http://dx.doi.org/10.1016/j.patcog.2007.06.029 PTNRA8 0031-3203 Google Scholar
S. L. Freeet al.,
“Methods for normalization of hippocampal volumes measured with MR,”
Am. J. Neuroradiol., 16
(4), 637
–643
(1995). 0195-6108 Google Scholar
S. R. KulkarniG. Harman,
“Statistical learning theory: a tutorial,”
Comput. Stat., 3
(6), 543
–556
(2011). http://dx.doi.org/10.1002/wics.v3.6 CSTAEB 0943-4062 Google Scholar
V. N. Vapnik, The Nature of Statistical Learning Theory, 2nd ed.Springer, New York
(2000). Google Scholar
C.-C. ChangC.-J. Lin,
“LIBSVM: a library for support vector machines,”
ACM Trans. Intell. Syst. Technol., 2
(3), 1
–27
(2011). http://dx.doi.org/10.1145/1961189.1961199 Google Scholar
J. Burges,
“A tutorial on support vector machines for pattern recognition,”
Data Mining Knowl. Discovery, 2
(2), 121
–167
(1988). http://dx.doi.org/10.1023/A:1009715923555 1384-5810 Google Scholar
C. Chih-ChungL. Chih-Jen,
“LIBSVM,”
(2013) http://www.csie.ntu.edu.tw/cjlin/libsvm/ Google Scholar
P. PudilJ. NovovicovaJ. Kittler,
“Floating search methods in feature selection,”
Pattern Recognit. Lett., 15
(11), 1119
–1125
(1994). http://dx.doi.org/10.1016/0167-8655(94)90127-9 PRLEDG 0167-8655 Google Scholar
S. J. Teipelet al.,
“Multicentre variability of MRI-based medial temporal lobe volumetry in Alzheimer’s disease,”
Psychiatry Res.: Neuroimaging, 182
(3), 244
–250
(2010). http://dx.doi.org/10.1016/j.pscychresns.2010.03.003 0925-4927 Google Scholar
A. B. TufailA. AbidiM. S. Younis,
“Multiclass classification of initial stages of Alzheimer’s disease using structural MRI phase images,”
in Proc. IEEE Int. Conf. on Control System, Computing and Engineering,
(2012). Google Scholar
T. ZhangC. Davatzikos,
“Optimally-discriminative voxel-based morphometry significantly increases the ability to detect group differences in schizophrenia, mild cognitive impairment, and Alzheimer’s disease,”
NeuroImage, 79
(1), 94
–110
(2013). http://dx.doi.org/10.1016/j.neuroimage.2013.04.063 NEIMEF 1053-8119 Google Scholar
J. Dukartet al.,
“Meta-analysis based SVM classification enables accurate detection of Alzheimer’s disease across different clinical center using FDG-PET and MRI,”
Psychiatry Res.: Neuroimaging, 212
(3), 230
–236
(2013). http://dx.doi.org/10.1016/j.pscychresns.2012.04.007 0925-4927 Google Scholar
J. Ramírezet al.,
“Computer-aided diagnosis of Alzheimer’s type dementia combining support vector machines and discriminant set of features,”
Inf. Sci., 237
(10), 59
–72
(2013). http://dx.doi.org/10.1016/j.ins.2009.05.012 0020-0255 Google Scholar
A. M. Torteyaet al.,
“MRI signal and texture features for the prediction of MCI to Alzheimer’s disease progression,”
Proc. SPIE, 9035 903526
(2014). http://dx.doi.org/10.1117/12.2043903 2329-4302 Google Scholar
BiographyJorge Luis Perez-Gonzalez is a PhD student in the doctoral program of biomedical engineering at the Universidad Autonoma Metropolitana, Mexico. He received his MSc degree in biomedical engineering from the Universidad Autonoma Metropolitana in 2013. His current research interests include medical image processing and analysis, computer-aided diagnosis, pattern recognition, and artificial intelligence. Oscar Yanez-Suarez has been at the Neuroimaging Laboratory, Department of Electrical Engineering of the Universidad Autonoma Metropolitana-Iztapalapa since 1989. He is actively involved in the undergraduate program in computer science and in both undergraduate and graduate programs in biomedical engineering. His research focuses on brain information processing, both from signals and images, and participates in diverse projects on statistical MRI segmentation, volumetric reconstructions, source estimation, and brain-computer interfaces. Ernesto Bribiesca received his BSc degree in electronics engineering from the IPN. He received his PhD degree in mathematics from the Universidad Autónoma Metropolitana in 1996, and he was a researcher at the IBM Latin American Scientific Center. He is an associate editor of Pattern Recognition. He has twice been chosen Honorable Mention winner of the Annual Pattern Recognition Society Award. Currently, he is a professor at the IIMAS at the Universidad Nacional Autónoma de México. Fernando Arámbula Cosío graduated with a PhD degree in advanced robotics from Imperial College of Science Technology and Medicine, London, UK, in 1997. He is a full-time lecturer at the Centre of Applied Science and Technological Development of the National Autonomous University of México (UNAM) since 1997. His main research interests are medical image analysis and computer-assisted surgery. Juan Ramón Jiménez is a professor in the Department of Electrical Engineering at Universidad Autónoma Metropolitana Iztapala. He has a PhD in biomedical engineering from the Universidad Autónoma Metropolitana. He works in the Research Laboratory of Neuroimaging in segmentation methods for MRI, image processing, clustering algorithms, data acquisition, and NIRS signal processing. He is a member of the IEEE and the Mexican Society of Biomedical Engineering. Veronica Medina-Bañuelos received her PhD degree in biomedical engineering from the Universite de Technologie de Compiegne, France, in 1991. For more than 30 years, she has been working for the Neuroimaging Laboratory at Universidad Autonoma Metropolitana-Iztapalapa, Mexico, where she served as a dean of the Basic Sciences and Engineering Division. She has published more than 50 peer-reviewed papers in medical signal and image processing, analysis, and pattern recognition and tutored more than 20 postgraduate students. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

